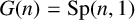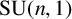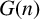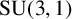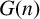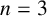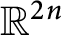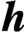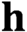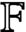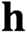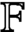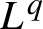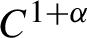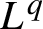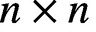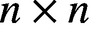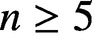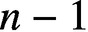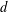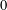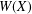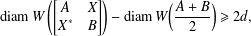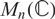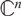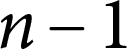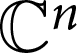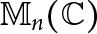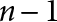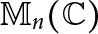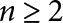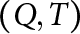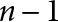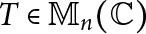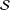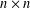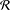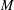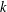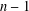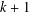Refine listing
Actions for selected content:
258 results in 15xxx
LOCAL COORDINATES FOR COMPLEX AND QUATERNIONIC HYPERBOLIC PAIRS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 57-78
- Print publication:
- August 2022
-
- Article
- Export citation
The polarization constant of finite dimensional complex spaces is one
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 105-123
- Print publication:
- January 2022
-
- Article
- Export citation
Some matrix inequalities of log-majorization type
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 95-105
- Print publication:
- March 2022
-
- Article
- Export citation
NONNEGATIVE POLYNOMIALS, SUMS OF SQUARES AND THE MOMENT PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 337-341
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
A NEW ALGORITHM FOR DECOMPOSING MODULAR TENSOR PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 11 January 2021, pp. 94-107
- Print publication:
- August 2021
-
- Article
- Export citation
Tight frames and related geometric problems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 942-963
- Print publication:
- December 2021
-
- Article
- Export citation
Inequalities on partial traces of positive semidefinite block matrices
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 964-969
- Print publication:
- December 2021
-
- Article
- Export citation
Derivatives of symplectic eigenvalues and a Lidskii type theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 02 December 2020, pp. 457-485
- Print publication:
- April 2022
-
- Article
-
- You have access
- Export citation
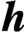 $\textit{h}$-MINIMUM SPANNING LENGTHS AND AN EXTENSION TO BURNSIDE’S THEOREM ON IRREDUCIBILITY
$\textit{h}$-MINIMUM SPANNING LENGTHS AND AN EXTENSION TO BURNSIDE’S THEOREM ON IRREDUCIBILITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 78-93
- Print publication:
- August 2021
-
- Article
- Export citation
FIXED POINT THEOREM FOR AN INFINITE TOEPLITZ MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 108-117
- Print publication:
- August 2021
-
- Article
- Export citation
MULTINOMIAL VANDERMONDE CONVOLUTION VIA PERMANENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 06 November 2020, pp. 353-361
- Print publication:
- June 2021
-
- Article
- Export citation
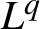 $L^{q}$-spectra of measures on planar non-conformal attractors
$L^{q}$-spectra of measures on planar non-conformal attractors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 3288-3306
- Print publication:
- November 2021
-
- Article
- Export citation
THE SLOT LENGTH OF A FAMILY OF MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 260-270
- Print publication:
- April 2021
-
- Article
- Export citation
Lineability, continuity, and antiderivatives in the non-Archimedean setting
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 02 September 2020, pp. 638-650
- Print publication:
- September 2021
-
- Article
- Export citation
Variational principles for symplectic eigenvalues
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 553-559
- Print publication:
- September 2021
-
- Article
- Export citation
NUMERICAL RANGE AND POSITIVE BLOCK MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 69-77
- Print publication:
- February 2021
-
- Article
- Export citation
HERMITIANS IN MATRIX ALGEBRAS WITH OPERATOR NORM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 27 April 2020, pp. 280-290
- Print publication:
- May 2021
-
- Article
- Export citation
The Distance from a Rank
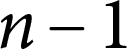 $n-1$ Projection to the Nilpotent Operators on
$n-1$ Projection to the Nilpotent Operators on 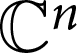 $\mathbb {C}^n$
$\mathbb {C}^n$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 02 April 2020, pp. 54-74
- Print publication:
- March 2021
-
- Article
- Export citation
Matrix Liberation Process II: Relation to Orbital Free Entropy
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 28 January 2020, pp. 493-541
- Print publication:
- April 2021
-
- Article
- Export citation
IRREDUCIBLE FAMILIES OF COMPLEX MATRICES CONTAINING A RANK-ONE MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 226-236
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation