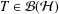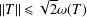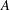Refine listing
Actions for selected content:
262 results in 15xxx
Efficient Preconditioner and Iterative Method for Large Complex Symmetric Linear Algebraic Systems
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 530-547
- Print publication:
- August 2017
-
- Article
- Export citation
Analysis of Hexagonal Grid Finite Difference Methods for Anisotropic Laplacian Related Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 562-596
- Print publication:
- August 2017
-
- Article
- Export citation
Numerical Ranges in II1 Factors
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 16 March 2017, pp. 31-55
-
- Article
- Export citation
The Disc Theorem for the Schur Complement of Two Class Submatrices with γ-Diagonally Dominant Properties
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 84-97
- Print publication:
- February 2017
-
- Article
- Export citation
The Explicit Inverses of CUPL-Toeplitz and CUPL-Hankel Matrices
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 38-54
- Print publication:
- February 2017
-
- Article
- Export citation
SOR-like Methods with Optimization Model for Augmented Linear Systems
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 101-115
- Print publication:
- February 2017
-
- Article
- Export citation
A Filtered-Davidson Method for Large Symmetric Eigenvalue Problems
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 21-37
- Print publication:
- February 2017
-
- Article
- Export citation
Convergence Rates of a Class of Predictor-Corrector Iterations for the Nonsymmetric Algebraic Riccati Equation Arising in Transport Theory
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 944-963
- Print publication:
- August 2017
-
- Article
- Export citation
A Robust and Efficient Adaptive Multigrid Solver for the Optimal Control of Phase Field Formulations of Geometric Evolution Laws
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 65-92
- Print publication:
- January 2017
-
- Article
- Export citation
OPERATOR QUASILINEARITY OF SOME FUNCTIONALS ASSOCIATED WITH DAVIS–CHOI–JENSEN’S INEQUALITY FOR POSITIVE MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 322-332
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
DASHMM: Dynamic Adaptive System for Hierarchical Multipole Methods
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 05 October 2016, pp. 1106-1126
- Print publication:
- October 2016
-
- Article
- Export citation
SOME INEQUALITIES FOR THE NUMERICAL RADIUS FOR HILBERT SPACE OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 26 September 2016, pp. 489-496
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
EXT-FINITE MODULES FOR WEAKLY SYMMETRIC ALGEBRAS WITH RADICAL CUBE ZERO
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 108-121
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
A MODIFIED FR CONJUGATE GRADIENT METHOD FOR COMPUTING
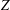 $Z$ -EIGENPAIRS OF SYMMETRIC TENSORS
$Z$ -EIGENPAIRS OF SYMMETRIC TENSORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 26 July 2016, pp. 411-420
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
RECFMM: Recursive Parallelization of the Adaptive Fast Multipole Method for Coulomb and Screened Coulomb Interactions
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 2 / August 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 534-550
- Print publication:
- August 2016
-
- Article
- Export citation
Convergence of an Anisotropic Perfectly Matched Layer Method for Helmholtz Scattering Problems
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 358-382
- Print publication:
- August 2016
-
- Article
- Export citation
A Block Diagonal Preconditioner for Generalised Saddle Point Problems
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 235-252
- Print publication:
- August 2016
-
- Article
- Export citation
Jacobi Spectral Collocation Method for the Time Variable-Order Fractional Mobile-Immobile Advection-Dispersion Solute Transport Model
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 337-352
- Print publication:
- August 2016
-
- Article
- Export citation
A Determinant Identity Implying the Lagrange–Good Inversion Formula
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 165-176
-
- Article
- Export citation
A fourth-order seven-point cubature on regular hexagons
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 175-185
-
- Article
-
- You have access
- Export citation