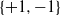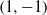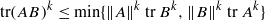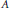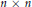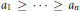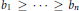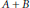Refine listing
Actions for selected content:
258 results in 15xxx
Cross-Commodity Spot Price Modeling with Stochastic Volatility and Leverage For Energy Markets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2016, pp. 545-571
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Pricing of Forwards and Options in a Multivariate Non-Gaussian Stochastic Volatility Model for Energy Markets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2016, pp. 572-594
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
TRACE INEQUALITIES AND A QUESTION OF BOURIN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 384-389
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
BOUNDS ON MINORS OF BINARY MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 23 December 2012, pp. 280-285
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Rational maps between quasilinear hypersurfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 17 December 2012, pp. 333-355
- Print publication:
- March 2013
-
- Article
- Export citation
INVERSE EIGENVALUE PROBLEM FOR EUCLIDEAN DISTANCE MATRICES OF SIZE 3
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 15 October 2012, pp. 82-93
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
TRACE INEQUALITIES FOR MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 139-148
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
REPRESENTATION THEOREMS FOR INDEFINITE QUADRATIC FORMS REVISITED
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 12 June 2012, pp. 169-189
- Print publication:
- January 2013
-
- Article
- Export citation
ASYMPTOTIC BEHAVIOUR OF RANDOM MARKOV CHAINS WITH TRIDIAGONAL GENERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 30 March 2012, pp. 27-36
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC ENUMERATION OF SYMMETRIC INTEGER MATRICES WITH UNIFORM ROW SUMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 04 March 2012, pp. 367-384
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
THE GENERALIZED SYLVESTER MATRIX EQUATION, RANK MINIMIZATION AND ROTH’S EQUIVALENCE THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 21 July 2011, pp. 441-443
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
ALGEBRAIC ASPECTS OF SPECTRAL THEORY
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 21 December 2010, pp. 63-88
- Print publication:
- January 2011
-
- Article
- Export citation
ON THE EXISTENCE OF NOWHERE-ZERO VECTORS FOR LINEAR TRANSFORMATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 14 September 2010, pp. 480-487
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
The Algebraic Degree of Phase-Type Distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 611-629
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
THE LINK BETWEEN REGULARITY AND STRONG-PI-REGULARITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 09 August 2010, pp. 17-22
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
GENERALIZED INVERSES OF A SUM IN RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 22 April 2010, pp. 156-164
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
Sum of Hermitian Matrices with Given Eigenvalues: Inertia, Rank, and Multiple Eigenvalues
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 109-132
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
ON THE LENGTHS OF PAIRS OF COMPLEX MATRICES OF SIZE SIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 08 June 2009, pp. 177-201
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
THE DRAZIN INVERSES OF PRODUCTS AND DIFFERENCES OF PROJECTIONS IN A C*-ALGEBRA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 189-198
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
A CANCELLATION PROPERTY OF THE MOORE–PENROSE INVERSE OF TRIPLE PRODUCTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 33-44
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation