Refine listing
Actions for selected content:
64 results in 28Dxx
STABLE SETS OF CERTAIN NON-UNIFORMLY HYPERBOLIC HORSESHOES HAVE THE EXPECTED DIMENSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 04 April 2019, pp. 305-329
- Print publication:
- January 2021
-
- Article
- Export citation
The
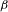 $\unicode[STIX]{x1D6FD}$-transformation with a hole at 0
$\unicode[STIX]{x1D6FD}$-transformation with a hole at 0
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2482-2514
- Print publication:
- September 2020
-
- Article
-
- You have access
- Open access
- Export citation
Nearly Approximate Transitivity (AT) for Circulant Matrices
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 381-415
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Local unstable entropies of partially hyperbolic diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 26 February 2019, pp. 2274-2304
- Print publication:
- August 2020
-
- Article
- Export citation
Return- and hitting-time distributions of small sets in infinite measure preserving systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 02 January 2019, pp. 2239-2273
- Print publication:
- August 2020
-
- Article
- Export citation
Geodesic Flows Modelled by Expansive Flows
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 61-95
-
- Article
- Export citation
On the Quantitative Metric Theory of Continued Fractions in Positive Characteristic
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 07 February 2018, pp. 283-293
-
- Article
-
- You have access
- Open access
- Export citation
KŐNIG’S LINE COLORING AND VIZING’S THEOREMS FOR GRAPHINGS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 19 September 2016, e27
-
- Article
-
- You have access
- Open access
- Export citation
Triangles in Cartesian Squares of Quasirandom Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 2 / March 2017
- Published online by Cambridge University Press:
- 25 August 2016, pp. 161-182
-
- Article
- Export citation
ON THE METRIC THEORY OF CONTINUED FRACTIONS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 27 May 2014, pp. 307-320
- Print publication:
- July 2014
-
- Article
-
- You have access
- Export citation
ON TENSOR PRODUCTS OF WEAK MIXING VECTOR SEQUENCES AND THEIR APPLICATIONS TO UNIQUELY E-WEAK MIXING C*-DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 04 October 2011, pp. 46-59
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
A Fourth Moment Inequality for Functionals of Stationary Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1086-1096
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
ON THE FUNDAMENTAL REGIONS OF A FIXED POINT FREE CONSERVATIVE HÉNON MAP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 37-48
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
Average co-ordinate entropy
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-186
- Print publication:
- October 2002
-
- Article
-
- You have access
- Export citation
β-transformation, invariant measure and uniform distribution
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 418-428
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
Dynamical systems defined on point processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 581-588
- Print publication:
- September 1998
-
- Article
- Export citation
Product and Markov measures of type III
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 84-110
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation
Strong shift equivalence of 2 by 2 non-negative integral matrices
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 302-312
- Print publication:
- December 1997
-
- Article
- Export citation
Odometer action on Riesz product
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-149
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
On diameters of orbits of compact groups in unitary representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 308-312
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
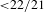
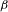
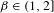
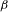
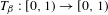
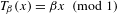
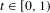
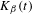
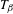
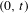
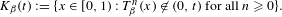
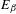
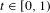
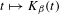
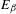
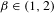
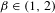
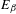
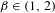
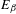

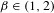
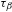
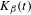
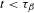
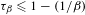
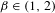
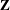
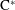
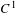
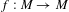
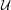
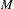
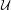
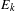
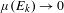



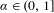

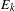
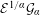
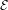
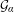
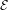
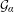

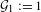
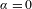
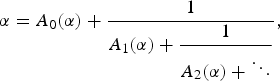
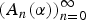
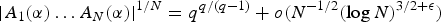
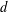
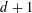
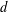
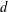
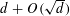
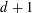
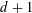
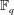
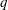

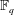
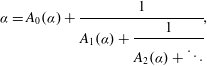
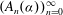
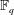
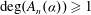
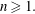
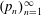
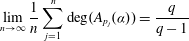

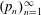
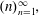
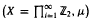 is introduced. This quantity-average co-ordinate or AC entropy-is calculated for product measures and
is introduced. This quantity-average co-ordinate or AC entropy-is calculated for product measures and 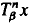 } are uniformly distributed. Here we consider the non-integer case, determine when
} are uniformly distributed. Here we consider the non-integer case, determine when 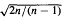 if
if 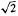 if
if 