Refine listing
Actions for selected content:
460 results in 28xxx
Complex extreme measurable selections
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 222-231
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
Insertion of a measurable function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-304
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
Dimension prints of fractal sets
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 68-94
- Print publication:
- June 1994
-
- Article
- Export citation
Sur une procédure de branchement déterministe et ses dérivées aléatoires
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 333-347
- Print publication:
- June 1994
-
- Article
- Export citation
On lattice-perfect measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 169-182
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Integration with respect to vector valued Radon polymeasures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 1 / February 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-40
- Print publication:
- February 1994
-
- Article
-
- You have access
- Export citation
Estimates of spherial averages of Fourier transforms and dimensions of sets
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 322-330
- Print publication:
- December 1993
-
- Article
- Export citation
Non-weak compactness of the integration map for vector measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 3 / June 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-303
- Print publication:
- June 1993
-
- Article
-
- You have access
- Export citation
Paradoxical decompositions using Lipschitz functions
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 216-222
- Print publication:
- December 1992
-
- Article
- Export citation
On the Lipschitz equivalence of Cantor sets
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 223-233
- Print publication:
- December 1992
-
- Article
- Export citation
Regular and ubiquitous systems, and ℳs∞-dense sequences
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 234-243
- Print publication:
- December 1992
-
- Article
- Export citation
Gaussian integrals on Wiener spaces
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 46-55
- Print publication:
- March 1992
-
- Article
- Export citation
Measures in banach spaces are determined by their values on balls
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 391-397
- Print publication:
- December 1991
-
- Article
- Export citation
Covering squares with independent squares
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 329-333
- Print publication:
- December 1991
-
- Article
- Export citation
Integral representation theorems in partially ordered vector spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-215
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
An ordered suprabarrelled space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 106-117
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
On the dimension of product measures
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 316-323
- Print publication:
- December 1990
-
- Article
- Export citation
Fractal series
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 2 / December 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 334-348
- Print publication:
- December 1989
-
- Article
- Export citation
Scaling Hausdorff measures
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 2 / December 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 325-333
- Print publication:
- December 1989
-
- Article
- Export citation
On measure derivation in metric spaces
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 2 / December 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 349-358
- Print publication:
- December 1989
-
- Article
- Export citation
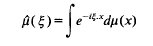
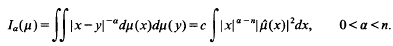
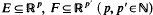 then
then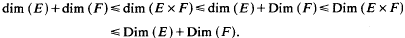
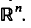 In Theorem 1 we give sufficient conditions for such series. Theorem 2 shows that each analytic function gives a different fractal series for each number in a certain open set. Theorem 3 gives the Hausdorff dimension of the associated sets to fractal series, under suitable conditions on the series. This theorem can be applied to some standard series in analysis, such as the binomial, exponential and trigonometrical complex series. The associated sets to geometrical complex series are selfsimilar sets previously studied by M. F. Barnsley from a different (dynamical) point of view (see refs. [5], [6]).
In Theorem 1 we give sufficient conditions for such series. Theorem 2 shows that each analytic function gives a different fractal series for each number in a certain open set. Theorem 3 gives the Hausdorff dimension of the associated sets to fractal series, under suitable conditions on the series. This theorem can be applied to some standard series in analysis, such as the binomial, exponential and trigonometrical complex series. The associated sets to geometrical complex series are selfsimilar sets previously studied by M. F. Barnsley from a different (dynamical) point of view (see refs. [5], [6]).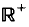 with θ(0)= 0 and let
with θ(0)= 0 and let 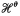 be the corresponding Hausdorff measure. We say that
be the corresponding Hausdorff measure. We say that 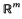 and
and