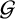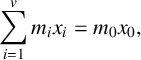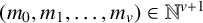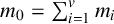Refine listing
Actions for selected content:
463 results in 28xxx
Do stable neural networks exist for classification problems? – A new view on stability in AI
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 20 November 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proof mining and probability theory
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 November 2025, e187
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak porosity on metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 November 2025, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the dimension theory of Okamoto’s function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE SHORTEST DISTANCE BETWEEN ORBITS IN CONFORMAL ITERATED FUNCTION SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-11
-
- Article
- Export citation
Quantization dimensions of negative order
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revisiting sums and products in countable and finite fields
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behavior for the sum of partial quotients in continued fraction expansions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1-13
-
- Article
- Export citation
Equidistribution in the complex plane and self-similar measures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-27
-
- Article
- Export citation
On the coincidence of the Hausdorff and box dimensions for some affine-invariant sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1-33
-
- Article
- Export citation
On the Assouad spectrum of Hölder and Sobolev graphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Petty projection inequality on the sphere and on the hyperbolic space
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 August 2025, pp. 1-28
-
- Article
- Export citation
Absolute continuity in the reproducing kernel sense
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ergodicity and algebraicity of the fast and slow triangle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-35
-
- Article
- Export citation
Regularity of non-autonomous self-similar sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 01 August 2025, pp. 623-648
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE SPECTRAL EIGENVALUES OF A CLASS OF PRODUCT-FORM SELF-SIMILAR SPECTRAL MEASURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 246-263
- Print publication:
- October 2025
-
- Article
- Export citation
DIMENSIONS OF SETS AVOIDING APPROXIMATE NONTRIVIAL ZEROS OF LINEAR PATTERNS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-12
-
- Article
- Export citation
DIMENSIONAL APPROXIMATION OF AN INHOMOGENEOUS ATTRACTOR WITHOUT ANY SEPARATION CONDITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. 515-527
- Print publication:
- December 2025
-
- Article
- Export citation
On Dirichlet non-improvable numbers and shrinking target problems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 11 June 2025, pp. 3540-3568
- Print publication:
- November 2025
-
- Article
- Export citation
Stable functional CLT for deterministic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 26 May 2025, pp. 3192-3222
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation