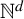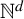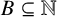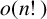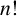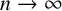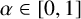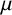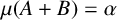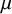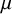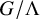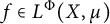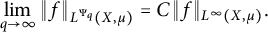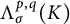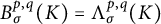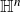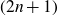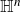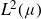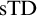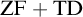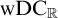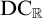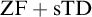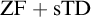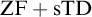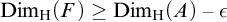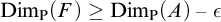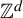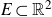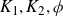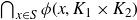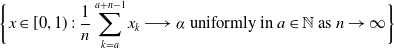Refine listing
Actions for selected content:
460 results in 28xxx
FRACTAL DIMENSIONS OF k-AUTOMATIC SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 25 July 2023, pp. 1128-1157
- Print publication:
- September 2024
-
- Article
- Export citation
‘A REMARKABLE ARTIFICE’: LAPLACE, POISSON AND MATHEMATICAL PURITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1018-1054
- Print publication:
- December 2024
-
- Article
- Export citation
Hausdorff dimension of multidimensional multiplicative subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1239-1268
- Print publication:
- May 2024
-
- Article
- Export citation
ON THE DENSITY OF SUMSETS, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 414-419
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak random periodic solutions of random dynamical systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 12 July 2023, pp. 137-151
- Print publication:
- March 2024
-
- Article
- Export citation
Expanding measures: Random walks and rigidity on homogeneous spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting periodic orbits on fractals weighted by their Lyapounov exponents
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 710-757
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multifractal analysis of sums of random pulses
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 22 June 2023, pp. 569-593
- Print publication:
- November 2023
-
- Article
- Export citation
Families of Young functions and limits of Orlicz norms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 26-39
- Print publication:
- March 2024
-
- Article
- Export citation
Equivalence of Besov spaces on p.c.f. self-similar sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1109-1143
- Print publication:
- August 2024
-
- Article
- Export citation
Necessary condition for the L2 boundedness of the Riesz transform on Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 23 May 2023, pp. 445-458
- Print publication:
- September 2023
-
- Article
- Export citation
SOME CONSEQUENCES OF
 ${\mathrm {TD}}$ AND
${\mathrm {TD}}$ AND 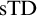 ${\mathrm {sTD}}$
${\mathrm {sTD}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1573-1589
- Print publication:
- December 2023
-
- Article
- Export citation
On sets with unit Hausdorff density in homogeneous groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 May 2023, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decomposition of multicorrelation sequences and joint ergodicity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 04 May 2023, pp. 432-480
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JARNÍK TYPE THEOREMS ON MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 25 April 2023, pp. 391-405
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Direct and inverse results for popular differences in trees of positive dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 April 2023, pp. 481-508
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Brownian motion on the golden ratio Sierpinski gasket
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 03 April 2023, pp. 699-726
- Print publication:
- June 2024
-
- Article
- Export citation
Finite point configurations in products of thick Cantor sets and a robust nonlinear Newhouse Gap Lemma
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 285-301
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff dimension of sets defined by almost convergent binary expansion sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 450-456
- Print publication:
- May 2023
-
- Article
- Export citation
Mixing properties of erasing interval maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 06 March 2023, pp. 408-431
- Print publication:
- February 2024
-
- Article
- Export citation