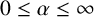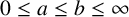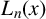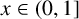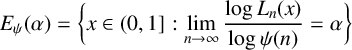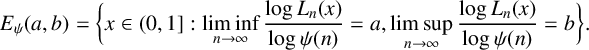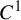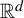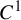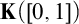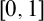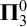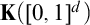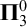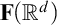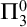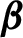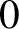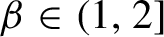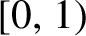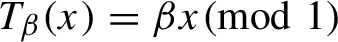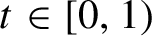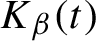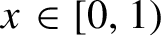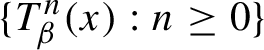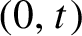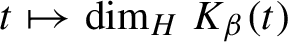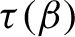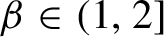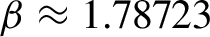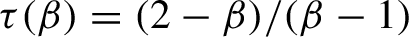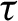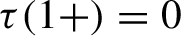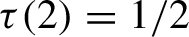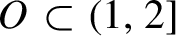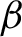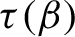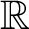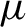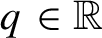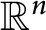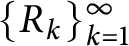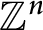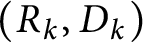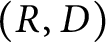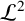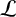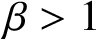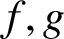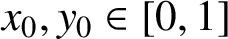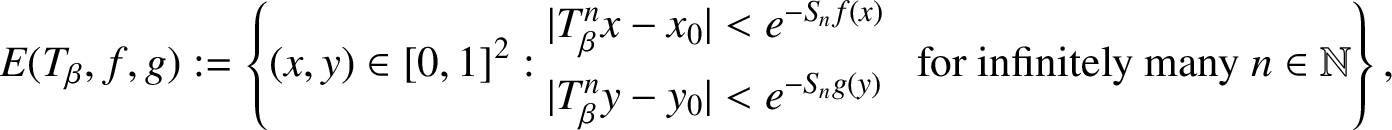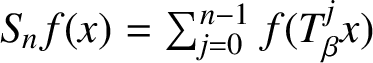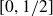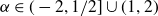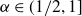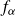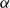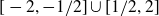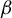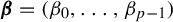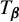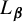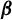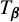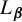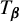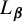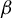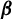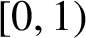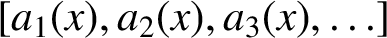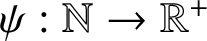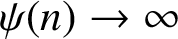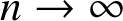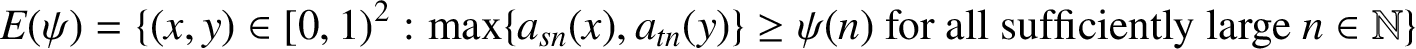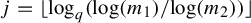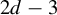Refine listing
Actions for selected content:
461 results in 28xxx
ON LÜROTH EXPANSIONS IN WHICH THE LARGEST DIGIT GROWS WITH SLOWLY INCREASING SPEED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 204-214
- Print publication:
- April 2023
-
- Article
- Export citation
Dimension estimates for
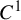 $C^1$ iterated function systems and repellers. Part I
$C^1$ iterated function systems and repellers. Part I
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 17 June 2022, pp. 2673-2706
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gradient estimation for smooth stopping criteria
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 15 June 2022, pp. 29-55
- Print publication:
- March 2023
-
- Article
- Export citation
Joint ergodicity of fractional powers of primes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The relative f-invariant and non-uniform random sofic approximations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 2073-2110
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A journey through computability, topology and analysis
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 June 2022, pp. 266-267
- Print publication:
- June 2022
-
- Article
-
- You have access
- Export citation
Critical values for the
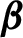 $\boldsymbol{\beta} $-transformation with a hole at
$\boldsymbol{\beta} $-transformation with a hole at 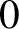 $0$
$0$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 02 May 2022, pp. 1785-1828
- Print publication:
- June 2023
-
- Article
- Export citation
Geometric and combinatorial properties of self-similar multifractal measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 27 April 2022, pp. 2028-2072
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectrality of a class of Moran measures on
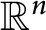 $\mathbb {R}^{n}$ with consecutive digit sets
$\mathbb {R}^{n}$ with consecutive digit sets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 April 2022, pp. 269-285
- Print publication:
- March 2023
-
- Article
- Export citation
A CONTINUOUS HOMOMORPHISM OF A THIN SET ONTO A FAT SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 01 April 2022, pp. 500-503
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological structure of the sum of two homogeneous Cantor sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 24 March 2022, pp. 1712-1736
- Print publication:
- May 2023
-
- Article
- Export citation
HIGHER-DIMENSIONAL SHRINKING TARGET PROBLEM FOR BETA DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 22 March 2022, pp. 289-311
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fractal projections with an application in number theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 16 March 2022, pp. 1760-1784
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EUCLIDEAN NUMBERS AND NUMEROSITIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 21 February 2022, pp. 112-146
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOOLEAN TYPES IN DEPENDENT THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 1349-1373
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Step roots of Littlewood polynomials and the extrema of functions in the Takagi class
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 591-618
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamical behavior of alternate base expansions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 22 December 2021, pp. 827-860
- Print publication:
- March 2023
-
- Article
- Export citation
ON THE INCREASING PARTIAL QUOTIENTS OF CONTINUED FRACTIONS OF POINTS IN THE PLANE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 December 2021, pp. 404-411
- Print publication:
- June 2022
-
- Article
- Export citation
Dimensions of ‘self-affine sponges’ invariant under the action of multiplicative integers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 14 December 2021, pp. 417-459
- Print publication:
- February 2023
-
- Article
- Export citation
SZEMERÉDI’S THEOREM: AN EXPLORATION OF IMPURITY, EXPLANATION, AND CONTENT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 December 2021, pp. 700-739
- Print publication:
- September 2023
-
- Article
- Export citation