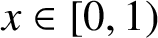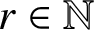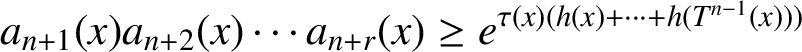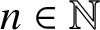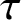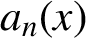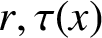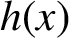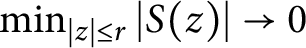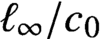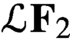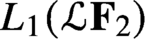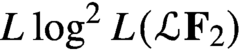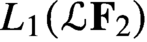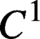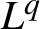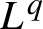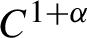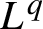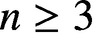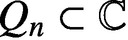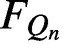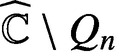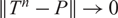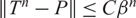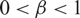Refine listing
Actions for selected content:
463 results in 28xxx
Hausdorff measure and Assouad dimension of generic self-conformal IFS on the line
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2051-2081
- Print publication:
- December 2021
-
- Article
- Export citation
HAUSDORFF DIMENSION FOR THE SET OF POINTS CONNECTED WITH THE GENERALIZED JARNÍK–BESICOVITCH SET
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 December 2020, pp. 1-29
- Print publication:
- February 2022
-
- Article
- Export citation
On the decay of singular inner functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 902-905
- Print publication:
- December 2021
-
- Article
- Export citation
Geometric functionals of fractal percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1085-1126
- Print publication:
- December 2020
-
- Article
- Export citation
The identity G(D)f = F for a linear partial differential operator G(D). Lusin type and structure results in the non-integrable case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 26 November 2020, pp. 1893-1919
- Print publication:
- December 2021
-
- Article
- Export citation
Noncommutative strong maximals and almost uniform convergence in several directions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 November 2020, e57
-
- Article
-
- You have access
- Open access
- Export citation
Product formalisms for measures on spaces with binary tree structures: representation, visualization, and multiscale noise
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e47
-
- Article
-
- You have access
- Open access
- Export citation
Erratum: Limiting properties of the distribution of primes in an arbitrarily large number of residue classes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 1041-1044
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
Number-theoretic positive entropy shifts with small centralizer and large normalizer
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 04 November 2020, pp. 3201-3226
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
A dichotomy of sets via typical differentiability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 November 2020, e41
-
- Article
-
- You have access
- Open access
- Export citation
A strongly irreducible affine iterated function system with two invariant measures of maximal dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3417-3438
- Print publication:
- November 2021
-
- Article
- Export citation
Cardinal invariants of Haar null and Haar meager sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1568-1594
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
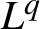 $L^{q}$-spectra of measures on planar non-conformal attractors
$L^{q}$-spectra of measures on planar non-conformal attractors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 3288-3306
- Print publication:
- November 2021
-
- Article
- Export citation
The Assouad spectrum of random self-affine carpets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 15 October 2020, pp. 2927-2945
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
EXISTENCE AND BOX DIMENSION OF GENERAL RECURRENT FRACTAL INTERPOLATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 278-290
- Print publication:
- April 2021
-
- Article
- Export citation
STARLIKENESS AND CONVEXITY OF CAUCHY TRANSFORMS ON REGULAR POLYGONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 291-302
- Print publication:
- April 2021
-
- Article
- Export citation
SPECTRAL CONDITIONS FOR UNIFORM P-ERGODICITIES OF MARKOV OPERATORS ON ABSTRACT STATES SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 23 September 2020, pp. 682-696
- Print publication:
- September 2021
-
- Article
- Export citation
BASES FOR FUNCTIONS BEYOND THE FIRST BAIRE CLASS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1289-1303
- Print publication:
- September 2020
-
- Article
- Export citation
Mixing and average mixing times for general Markov processes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 14 August 2020, pp. 541-552
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
ON GILP’S GROUP-THEORETIC APPROACH TO FALCONER’S DISTANCE PROBLEM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 28 July 2020, pp. 547-562
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation