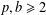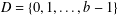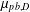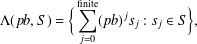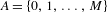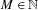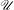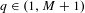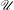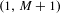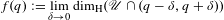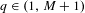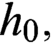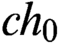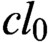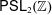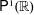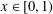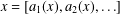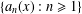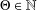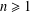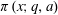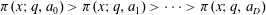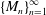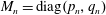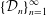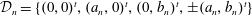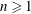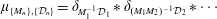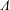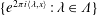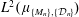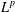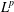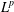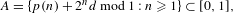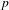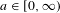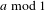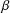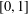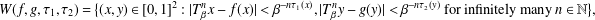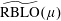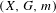Refine listing
Actions for selected content:
463 results in 28xxx
Extremality and dynamically defined measures, part II: Measures from conformal dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 30 June 2020, pp. 2311-2348
- Print publication:
- August 2021
-
- Article
- Export citation
NUMBER THEORY PROBLEMS RELATED TO THE SPECTRUM OF CANTOR-TYPE MEASURES WITH CONSECUTIVE DIGITS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 10 June 2020, pp. 113-123
- Print publication:
- February 2021
-
- Article
- Export citation
A new characterization of the Haagerup property by actions on infinite measure spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 2349-2368
- Print publication:
- August 2021
-
- Article
- Export citation
Estimates for sums and gaps of eigenvalues of Laplacians on measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 842-861
- Print publication:
- April 2021
-
- Article
- Export citation
Relative bifurcation sets and the local dimension of univoque bases
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 26 May 2020, pp. 2241-2273
- Print publication:
- August 2021
-
- Article
- Export citation
INNER AMENABLE GROUPOIDS AND CENTRAL SEQUENCES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 May 2020, e29
-
- Article
-
- You have access
- Open access
- Export citation
AN APPLICATION OF RECURSION THEORY TO ANALYSIS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 11 June 2020, pp. 15-25
- Print publication:
- March 2020
-
- Article
- Export citation
NONMEASURABLE SETS AND UNIONS WITH RESPECT TO TREE IDEALS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 19 June 2020, pp. 1-14
- Print publication:
- March 2020
-
- Article
- Export citation
MEASURABLE REALIZATIONS OF ABSTRACT SYSTEMS OF CONGRUENCES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 24 February 2020, e10
-
- Article
-
- You have access
- Open access
- Export citation
ON THE LONGEST BLOCK FUNCTION IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 196-206
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
On intrinsic and extrinsic rational approximation to Cantor sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 10 February 2020, pp. 1560-1589
- Print publication:
- May 2021
-
- Article
- Export citation
Limiting Properties of the Distribution of Primes in an Arbitrarily Large Number of Residue Classes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 837-849
- Print publication:
- December 2020
-
- Article
- Export citation
Spectrality of a Class of Moran Measures
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 17 January 2020, pp. 366-381
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
COMPACT WEIGHTED COMPOSITION OPERATORS BETWEEN
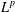 $L^{p}$-SPACES
$L^{p}$-SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 151-161
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Bernoulli decomposition and arithmetical independence between sequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 14 January 2020, pp. 1590-1600
- Print publication:
- May 2021
-
- Article
-
- You have access
- Open access
- Export citation
SIMULTANEOUS DYNAMICAL DIOPHANTINE APPROXIMATION IN BETA EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 186-195
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Assouad Spectrum Thresholds for Some Random Constructions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 12 December 2019, pp. 434-453
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
The John–Nirenberg Inequality for the Regularized BLO Space on Non-homogeneous Metric Measure Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 643-654
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
An autocorrelation and a discrete spectrum for dynamical systems on metric spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 27 November 2019, pp. 906-922
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation
Lower Assouad Dimension of Measures and Regularity
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 22 November 2019, pp. 379-415
- Print publication:
- March 2021
-
- Article
- Export citation