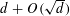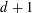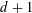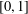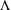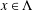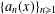Refine listing
Actions for selected content:
462 results in 28xxx
Assouad dimensions of complementary sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 12 April 2018, pp. 517-540
- Print publication:
- June 2018
-
- Article
- Export citation
A mass transference principle for systems of linear forms and its applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1014-1047
- Print publication:
- May 2018
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Recurrence to Shrinking Targets on Typical Self-Affine Fractals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 387-400
-
- Article
- Export citation
On the Quantitative Metric Theory of Continued Fractions in Positive Characteristic
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 07 February 2018, pp. 283-293
-
- Article
-
- You have access
- Open access
- Export citation
Local Fractal Interpolation on Unbounded Domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 23 January 2018, pp. 151-167
-
- Article
- Export citation
HAUSDORFF DIMENSION OF THE SET APPROXIMATED BY IRRATIONAL ROTATIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 267-283
- Print publication:
- 2018
-
- Article
- Export citation
A UNIFIED APPROACH TO CONTINUOUS, MEASURABLE SELECTIONS, AND SELECTIONS FOR HYPERSPACES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 607-627
- Print publication:
- 2018
-
- Article
- Export citation
ON THE
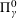 $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS AND
$\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS AND 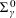 $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$ -COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 06 February 2018, pp. 77-114
- Print publication:
- 2018
-
- Article
- Export citation
LIPSCHITZ EQUIVALENCE OF CANTOR SETS AND IRREDUCIBILITY OF POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 26 June 2018, pp. 730-741
- Print publication:
- 2018
-
- Article
- Export citation
DENSITY, SMITAL PROPERTY AND QUASICONTINUITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 246-252
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
TWO-DIMENSIONAL SHRINKING TARGET PROBLEM IN BETA-DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 33-42
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
CHARACTERIZATIONS OF THE BOREL
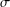 $\unicode[STIX]{x1D70E}$ -FIELDS OF THE FUZZY NUMBER SPACE
$\unicode[STIX]{x1D70E}$ -FIELDS OF THE FUZZY NUMBER SPACE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 265-275
-
- Article
-
- You have access
- Export citation
COEFFICIENT ESTIMATES FOR SOME CLASSES OF FUNCTIONS ASSOCIATED WITH
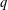 $q$ -FUNCTION THEORY
$q$ -FUNCTION THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 446-456
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Lacunary Interpolation by Fractal Splines with Variable Scaling Parameters
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 65-83
- Print publication:
- February 2017
-
- Article
- Export citation
A Fractal Operator on Some Standard Spaces of Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 771-786
-
- Article
- Export citation
A REPRESENTATION FOR THE INVERSE GENERALISED FOURIER–FEYNMAN TRANSFORM VIA CONVOLUTION PRODUCT ON FUNCTION SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 424-435
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
On the Global Gaussian Lipschitz Space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 03 January 2017, pp. 707-720
-
- Article
- Export citation
BOUNDARY PARAMETRIZATION AND THE TOPOLOGY OF TILES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 226 / June 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 127-164
- Print publication:
- June 2017
-
- Article
-
- You have access
- HTML
- Export citation
KŐNIG’S LINE COLORING AND VIZING’S THEOREMS FOR GRAPHINGS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 19 September 2016, e27
-
- Article
-
- You have access
- Open access
- Export citation
ON POINTS WITH POSITIVE DENSITY OF THE DIGIT SEQUENCE IN INFINITE ITERATED FUNCTION SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 435-443
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
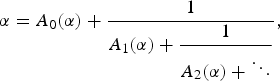
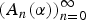
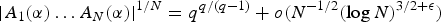
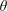
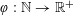


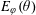

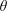
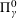
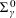
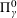
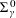
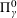
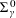
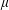
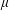
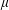
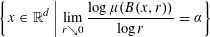
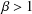
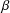
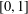
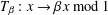
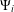
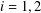
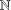
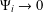
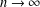
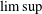
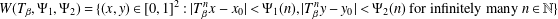
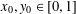
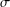
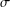
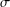
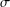
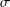
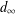
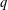
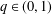







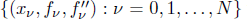 with equally spaced knot sequence in the unit interval, we show the existence of a family of fractal splines
with equally spaced knot sequence in the unit interval, we show the existence of a family of fractal splines 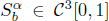 satisfying
satisfying 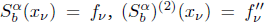 for
for 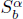 satisfies
satisfies 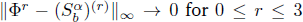 , as the number of partition points increases.
, as the number of partition points increases. , the space of all real-valued continuous functions defined on a compact interval
, the space of all real-valued continuous functions defined on a compact interval 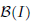 of all bounded functions and the Lebesgue space
of all bounded functions and the Lebesgue space 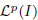 , and in some standard spaces of smooth functions such as the space
, and in some standard spaces of smooth functions such as the space 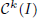 of
of 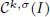 and Sobolev spaces
and Sobolev spaces 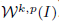 . Using properties of the
. Using properties of the 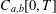
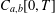
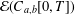
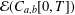
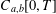
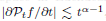 , where
, where 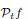 is the Poisson integral of the function
is the Poisson integral of the function