Refine listing
Actions for selected content:
463 results in 28xxx
FRACTAL BASES FOR BANACH SPACES OF SMOOTH FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 405-419
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
A NOTE ON SOME TOPOLOGICAL PROPERTIES OF SETS WITH FINITE PERIMETER
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 23 July 2015, pp. 637-647
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
On a measure-theoretic area formula
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 4 / August 2015
- Published online by Cambridge University Press:
- 20 July 2015, pp. 885-891
- Print publication:
- August 2015
-
- Article
- Export citation
MULTIFRACTAL ANALYSIS OF FUNCTIONS ON HEISENBERG AND CARNOT GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 27 March 2015, pp. 1-38
- Print publication:
- February 2017
-
- Article
- Export citation
FRACTAL INTERPOLATION SURFACES ON RECTANGULAR GRIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 435-446
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
First-Order Convergence and Roots†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 24 February 2015, pp. 213-221
-
- Article
- Export citation
WEIGHTED ESTIMATES ON FRACTAL DOMAINS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 03 February 2015, pp. 370-384
- Print publication:
- May 2015
-
- Article
- Export citation
CONCAVITY PROPERTIES OF EXTENSIONS OF THE PARALLEL VOLUME
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 13 January 2015, pp. 266-282
- Print publication:
- 2016
-
- Article
- Export citation
Hidden regular variation of moving average processes with heavy-tailed innovations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 267-279
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A Frostman-Type Lemma for Sets with Large Intersections, and an Application to Diophantine Approximation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 521-542
-
- Article
-
- You have access
- Export citation
Krein-Smulian-Type Theorems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 441-444
-
- Article
-
- You have access
- Export citation
HAUSDORFF DIMENSIONS OF SOME LIMINF SETS IN DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 17 September 2014, pp. 101-120
- Print publication:
- January 2015
-
- Article
- Export citation
A NOTE ON INHOMOGENEOUS DIOPHANTINE APPROXIMATION IN BETA-DYNAMICAL SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 12 September 2014, pp. 34-40
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
ON THE METRIC THEORY OF CONTINUED FRACTIONS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 27 May 2014, pp. 307-320
- Print publication:
- July 2014
-
- Article
-
- You have access
- Export citation
METRIC DIFFERENTIABILITY OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 15 October 2013, pp. 25-35
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
APPROXIMATING THE KOHLRAUSCH FUNCTION BY SUMS OF EXPONENTIALS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. 306-323
-
- Article
-
- You have access
- Export citation
THE CONLEY ATTRACTORS OF AN ITERATED FUNCTION SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 11 June 2013, pp. 267-279
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
WEAK CONTINUITY OF THE COMPLEX
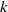 $k$-HESSIAN OPERATORS WITH RESPECT TO LOCAL UNIFORM CONVERGENCE
$k$-HESSIAN OPERATORS WITH RESPECT TO LOCAL UNIFORM CONVERGENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 11 June 2013, pp. 227-233
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
SUBGROUPS OF FRACTIONAL DIMENSION IN NILPOTENT OR SOLVABLE LIE GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 23 May 2013, pp. 497-511
- Print publication:
- July 2013
-
- Article
- Export citation
ON THE DIOPHANTINE PROPERTIES OF λ-EXPANSIONS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 65-86
- Print publication:
- January 2013
-
- Article
- Export citation
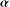
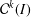
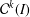
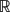
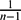
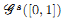 of subsets of [0, 1], originally introduced by Falconer, that are closed under countable intersections, and such that every set in the class has Hausdorff dimension at least
of subsets of [0, 1], originally introduced by Falconer, that are closed under countable intersections, and such that every set in the class has Hausdorff dimension at least 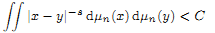
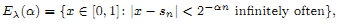
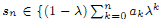 and
and 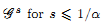 . This improves one of our previously published results.
. This improves one of our previously published results.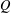
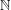
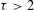
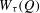
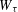

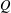
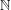
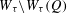
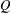
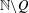
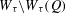
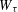
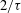
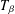
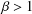
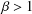
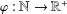
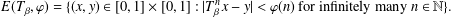

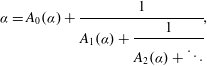
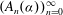
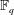
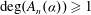
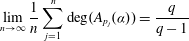

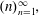
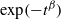
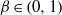
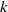
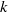
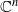
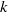
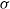
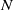
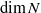
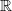
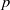
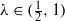 and
and 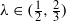 , the upper bound of
, the upper bound of 