Refine listing
Actions for selected content:
460 results in 28xxx
Sums of Cantor sets yielding an interval
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-418
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
Average co-ordinate entropy
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 2 / October 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-186
- Print publication:
- October 2002
-
- Article
-
- You have access
- Export citation
Generalized vector multiplicative cascades
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 874-895
- Print publication:
- December 2001
-
- Article
- Export citation
The bounded vector measure associated to a conical measure and pettis differentiability
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 10-36
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
Random fractals and probability metrics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 925-947
- Print publication:
- December 2000
-
- Article
- Export citation
N-fold sums of Cantor sets
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 243-250
- Print publication:
- December 2000
-
- Article
- Export citation
Density and covering properties of intervals of ℝn
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-242
- Print publication:
- December 2000
-
- Article
- Export citation
Fubini-type theorems for general measure constructions
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 251-265
- Print publication:
- December 2000
-
- Article
- Export citation
A central limit theorem for iterated random functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 748-755
- Print publication:
- September 2000
-
- Article
- Export citation
Compact measure spaces
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 331-336
- Print publication:
- December 1999
-
- Article
- Export citation
On the convergence of Σ∞n = 1f(nx) for measurable functions
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 337-341
- Print publication:
- December 1999
-
- Article
- Export citation
β-transformation, invariant measure and uniform distribution
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 418-428
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
Fractal n-hedral tilings of ℝd
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 403-417
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
A Radon-Nikodým theorem for vector polymeasures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 2 / April 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-200
- Print publication:
- April 1999
-
- Article
-
- You have access
- Export citation
The convex hull of samples from self-similar distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 34-47
- Print publication:
- March 1999
-
- Article
- Export citation
Dynamical systems defined on point processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 581-588
- Print publication:
- September 1998
-
- Article
- Export citation
Product and Markov measures of type III
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 84-110
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation
Hausdorff and packing dimensions and sections of measures
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 55-77
- Print publication:
- June 1998
-
- Article
- Export citation
No b-concentrated measures whenever 1<b≤2
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 37-41
- Print publication:
- June 1998
-
- Article
- Export citation
A relationship between packing and topological dimensions
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 43-53
- Print publication:
- June 1998
-
- Article
- Export citation
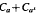 is an interval if and only if a /(1−2
is an interval if and only if a /(1−2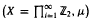 is introduced. This quantity-average co-ordinate or AC entropy-is calculated for product measures and
is introduced. This quantity-average co-ordinate or AC entropy-is calculated for product measures and 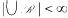 , then there is a finite sequence
, then there is a finite sequence 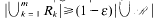 and
and 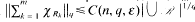 .
.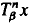 } are uniformly distributed. Here we consider the non-integer case, determine when
} are uniformly distributed. Here we consider the non-integer case, determine when 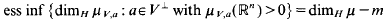
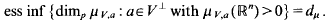
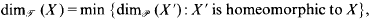
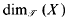 and
and 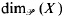 denote the topological and packing dimensions of
denote the topological and packing dimensions of 