Refine listing
Actions for selected content:
460 results in 28xxx
Measures on two-dimensional products
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 2 / December 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 253-258
- Print publication:
- December 1989
-
- Article
- Export citation
Continuity properties of the superposition operator
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 186-210
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
Some topological properties of vector measures and their integral maps: Errata
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 3 / December 1988
- Published online by Cambridge University Press:
- 09 April 2009, p. 371
- Print publication:
- December 1988
-
- Article
-
- You have access
- Export citation
Openness of vector measures and their integral maps
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 3 / December 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 351-359
- Print publication:
- December 1988
-
- Article
-
- You have access
- Export citation
Ergodic measures for the irrational rotation on the circle
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 133-141
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
Dimension prints
- Part of
-
- Journal:
- Mathematika / Volume 35 / Issue 1 / June 1988
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-27
- Print publication:
- June 1988
-
- Article
- Export citation
Spherical averages of Fourier transforms of measures with finite energy; dimensions of intersections and distance sets
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 2 / December 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 207-228
- Print publication:
- December 1987
-
- Article
- Export citation
Families of plane curves having translates in a set of measure zero
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 1 / June 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 69-76
- Print publication:
- June 1987
-
- Article
- Export citation
A concrete realization of the dual space of L1-spaces of certain vector and operator-valued measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 265-279
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
On strong lifting compactness, with applications to topological vector spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 211-223
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
A Riemann integral in a locally compact Hausdorff space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 1 / August 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 115-137
- Print publication:
- August 1986
-
- Article
-
- You have access
- Export citation
A survey of intergration by parts for Perron integrals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 3 / June 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 343-363
- Print publication:
- June 1986
-
- Article
-
- You have access
- Export citation
Non-σ-finite sets for packing measure
- Part of
-
- Journal:
- Mathematika / Volume 33 / Issue 1 / June 1986
- Published online by Cambridge University Press:
- 26 February 2010, pp. 129-136
- Print publication:
- June 1986
-
- Article
- Export citation
On vector lattice-valued measures II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 234-252
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
Orbit entropy in noninvertible mappings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 1 / February 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 95-110
- Print publication:
- February 1986
-
- Article
-
- You have access
- Export citation
On the Hausdorff dimensions of distance sets
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 206-212
- Print publication:
- December 1985
-
- Article
- Export citation
The range of an o-weakly compact mapping
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 3 / December 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 391-399
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
Classes of sets with large intersection
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 2 / December 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 191-205
- Print publication:
- December 1985
-
- Article
- Export citation
Measures coniques sur un espace de Banach ou son dual
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 39-50
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
Extending classical criteria for differentiation theorems
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 68-74
- Print publication:
- June 1985
-
- Article
- Export citation
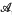 , μ,) and (
, μ,) and (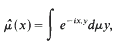
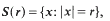
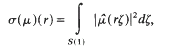
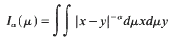
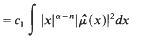
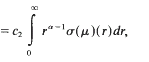
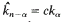 where
where 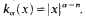 .
.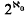 disjoint compact subsets each of non-σ-finite measure. The corresponding problem for Hausdorff measures is discussed, but not completely resolved, in Rogers' book [7]. We also show that packing measure cannot be attained by taking the Hausdorff measure with respect to a different increasing function using another metric which generates the same topology. This means that the class of pacing measures is distinct from the class of Hausdorff measures.
disjoint compact subsets each of non-σ-finite measure. The corresponding problem for Hausdorff measures is discussed, but not completely resolved, in Rogers' book [7]. We also show that packing measure cannot be attained by taking the Hausdorff measure with respect to a different increasing function using another metric which generates the same topology. This means that the class of pacing measures is distinct from the class of Hausdorff measures.