Refine listing
Actions for selected content:
460 results in 28xxx
A CHARACTERIZATION OF THE WEAK RADON–NIKODÝM PROPERTY BY FINITELY ADDITIVE INTERVAL FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 07 September 2009, pp. 476-485
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
SOME EXAMPLES IN VECTOR INTEGRATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 29 June 2009, pp. 384-392
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
PRODUCT FRACTAL SETS DETERMINED BY STABLE PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 26 February 2009, pp. 201-212
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
REVERSE ITERATED FUNCTION SYSTEM AND DIMENSION OF DISCRETE FRACTALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 37-47
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
CONDITIONAL FEYNMAN INTEGRAL AND SCHRÖDINGER INTEGRAL EQUATION ON A FUNCTION SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 10 March 2009, pp. 1-22
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
p-VARIATION OF VECTOR MEASURES WITH RESPECT TO BILINEAR MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 411-430
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
A Fourth Moment Inequality for Functionals of Stationary Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1086-1096
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
A Compact Framework for Hidden Markov Chains with Applications to Fractal Geometry
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 630-639
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
ON THE FUNDAMENTAL REGIONS OF A FIXED POINT FREE CONSERVATIVE HÉNON MAP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 37-48
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
The Hausdorff dimension of a class of random self-similar fractal trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 708-730
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Renewal of singularity sets of random self-similar measures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 162-188
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Spaces of vector functions that are integrable with respect to vector measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 85-109
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
On Infinitesimal Increase of Volumes of Morphological Transforms
- Part of
-
- Journal:
- Mathematika / Volume 53 / Issue 1 / June 2006
- Published online by Cambridge University Press:
- 21 December 2009, pp. 103-127
- Print publication:
- June 2006
-
- Article
- Export citation
Families of surfaces lying in a null set
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-162
- Print publication:
- December 2004
-
- Article
- Export citation
Ergodicity and stability of orbits of unbounded semigroup representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 209-232
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
Bilinear integration with positive vector measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 279-294
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
Multiplicities of Higher Lie Characters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 9-21
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Engel Series Expansions of Laurent Series and Hausdorff Dimensions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-7
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Joint continuity of injective tensor products of vector measures in Banach lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 185-200
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Thick and thin points for random recursive fractals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 251-277
- Print publication:
- March 2003
-
- Article
- Export citation
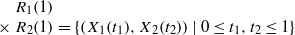 . The result of Hu generalizes [Some fractal sets determined by stable processes,
. The result of Hu generalizes [Some fractal sets determined by stable processes, 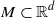 . An invariant set is defined to be a nonempty set
. An invariant set is defined to be a nonempty set 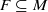 satisfying
satisfying 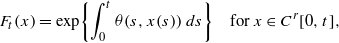
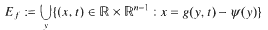
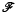 , the reduced Beurling spectrum of ø is empty if and only if ø ∈
, the reduced Beurling spectrum of ø is empty if and only if ø ∈ 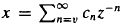 in an inderminate
in an inderminate 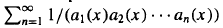 be the Engel expansin of Laurent series of
be the Engel expansin of Laurent series of 