Refine listing
Actions for selected content:
462 results in 28xxx
Spectrality of self-affine measures on the three-dimensional Sierpinski gasket
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 20 April 2012, pp. 477-496
-
- Article
-
- You have access
- Export citation
Visible parts of fractal percolation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 311-331
-
- Article
-
- You have access
- Export citation
SPARSE SETS ON THE PLANE AND DENSITY POINTS DEFINED BY FAMILIES OF SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 06 March 2012, pp. 282-290
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
A VARIATIONAL McSHANE INTEGRAL CHARACTERISATION OF THE WEAK RADON–NIKODYM PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 21 February 2012, pp. 456-462
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
ON THE MARGINALS OF PROBABILITY CONTENTS ON LATTICES
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 06 February 2012, pp. 319-323
- Print publication:
- July 2012
-
- Article
- Export citation
POLAR DECOMPOSITION OF THE k-FOLD PRODUCT OF LEBESGUE MEASURE ON ℝn
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 06 January 2012, pp. 315-324
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
The Darboux problem involving the distributional Henstock–Kurzweil integral
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 04 January 2012, pp. 197-205
-
- Article
-
- You have access
- Export citation
LEAST SQUARES APPROXIMATIONS OF MEASURES VIA GEOMETRIC CONDITION NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 20 December 2011, pp. 45-70
- Print publication:
- January 2012
-
- Article
- Export citation
TWO NONTRIVIAL WEAK SOLUTIONS FOR THE DIRICHLET PROBLEM ON THE SIERPIŃSKI GASKET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 12 December 2011, pp. 395-414
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
BALANCED CONVEX PARTITIONS OF MEASURES IN ℝd
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 21 October 2011, pp. 71-76
- Print publication:
- January 2012
-
- Article
- Export citation
ON TENSOR PRODUCTS OF WEAK MIXING VECTOR SEQUENCES AND THEIR APPLICATIONS TO UNIQUELY E-WEAK MIXING C*-DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 04 October 2011, pp. 46-59
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
NOTE ABOUT LINDELÖF Σ-SPACES υX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 28 September 2011, pp. 114-120
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
On Hölder continuity-in-time of the optimal transport map towards measures along a curve
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 31 March 2011, pp. 401-409
-
- Article
-
- You have access
- Export citation
Curves of infinite length in labyrinth fractals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 329-344
-
- Article
-
- You have access
- Export citation
Multifractal spectra for random self-similar measures via branching processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-39
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
SPECTRAL GAP FOR SOME INVARIANT LOG-CONCAVE PROBABILITY MEASURES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 22 November 2010, pp. 51-62
- Print publication:
- January 2011
-
- Article
- Export citation
The spectra of the Laplacians of fractal graphs not satisfying spectral decimation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 731-746
-
- Article
-
- You have access
- Export citation
Upper conical density results for general measures on ℝn
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 311-331
-
- Article
-
- You have access
- Export citation
SOLUTIONS OF A GOŁA̧B–SCHINZEL-TYPE FUNCTIONAL EQUATION BOUNDED ON ‘BIG’ SETS IN AN ABSTRACT SENSE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 05 March 2010, pp. 430-441
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Simultaneous Multifractal Analysis of the Branching and Visibility Measure on a Galton-Watson Tree
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 226-245
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
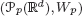 ). We prove that in most cases such a map is no more than 1/
). We prove that in most cases such a map is no more than 1/