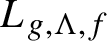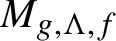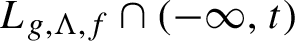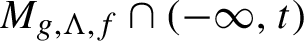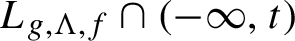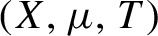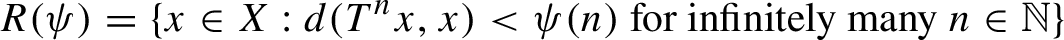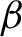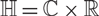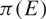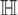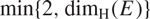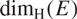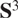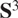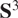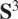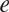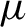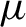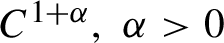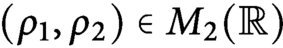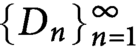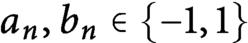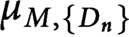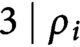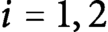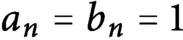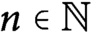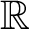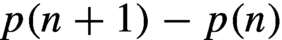Refine listing
Actions for selected content:
462 results in 28xxx
Continuity of Hausdorff dimension across generic dynamical Lagrange and Markov spectra II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 1898-1907
- Print publication:
- June 2022
-
- Article
- Export citation
Flexibility of measure-theoretic entropy of boundary maps associated to Fuchsian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 14 April 2021, pp. 389-401
- Print publication:
- February 2022
-
- Article
- Export citation
Porosity in Conformal Dynamical Systems
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 14 April 2021, pp. 303-371
- Print publication:
- March 2022
-
- Article
- Export citation
Dynamical Borel–Cantelli lemma for recurrence theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 12 April 2021, pp. 1994-2008
- Print publication:
- June 2022
-
- Article
- Export citation
On the dimension of points which escape to infinity at given rate under exponential iteration
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 29 March 2021, pp. 1591-1623
- Print publication:
- May 2022
-
- Article
- Export citation
Groups with infinite FC-center have the Schmidt property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 17 March 2021, pp. 1662-1707
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
Projections of Poisson cut-outs in the Heisenberg group and the visual 3-sphere
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 March 2021, pp. 197-230
- Print publication:
- January 2022
-
- Article
- Export citation
Entropy of killed-resurrected stationary Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 177-196
- Print publication:
- March 2021
-
- Article
- Export citation
RECURRENCE AND THE EXISTENCE OF INVARIANT MEASURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 60-76
- Print publication:
- March 2021
-
- Article
- Export citation
Combinatorial proofs of two theorems of Lutz and Stull
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 503-514
- Print publication:
- November 2021
-
- Article
- Export citation
Entropies and volume growth of unstable manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 04 February 2021, pp. 1576-1590
- Print publication:
- April 2022
-
- Article
- Export citation
Minimal definable graphs of definable chromatic number at least three
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 28 January 2021, e7
-
- Article
-
- You have access
- Open access
- Export citation
Spectrality of Moran Sierpinski-type measures on
 ${\mathbb R}^2$
${\mathbb R}^2$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 1024-1040
- Print publication:
- December 2021
-
- Article
- Export citation
Boxes, extended boxes and sets of positive upper density in the Euclidean space
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 481-501
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
Dispersive fractalisation in linear and nonlinear Fermi–Pasta–Ulam–Tsingou lattices
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 12 January 2021, pp. 820-845
-
- Article
-
- You have access
- Open access
- Export citation
SHORTENING CLOPEN GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1541-1554
- Print publication:
- December 2021
-
- Article
- Export citation
Invariant densities for random systems of the interval
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 141-179
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
The number of ergodic measures for transitive subshifts under the regular bispecial condition
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 86-140
- Print publication:
- January 2022
-
- Article
- Export citation
Uniformly positive entropy of induced transformations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 9-18
- Print publication:
- January 2022
-
- Article
- Export citation
Hausdorff measure and Assouad dimension of generic self-conformal IFS on the line
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2051-2081
- Print publication:
- December 2021
-
- Article
- Export citation