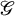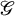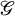Refine listing
Actions for selected content:
315 results in 17xxx
Cohomology of restricted twisted Heisenberg Lie algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 November 2025, pp. 1-12
-
- Article
- Export citation
Correction to “Irreducible modules of modular Lie superalgebras and super version of the first Kac-Weisfeiler conjecture”
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 October 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Cohomologies, deformations and abelian extensions of Lie super triple systems with superderivations
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 01 October 2025, pp. 1-22
-
- Article
- Export citation
Symmetric Hom–Leibniz algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 29 September 2025, pp. 1-24
-
- Article
- Export citation
Corrigendum: “On the representability of actions of Leibniz algebras and Poisson algebras”
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1419-1420
-
- Article
-
- You have access
- HTML
- Export citation
BUBBLES IN THE AFFINE BRAUER AND KAUFFMAN CATEGORIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 September 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON REPRESENTATIONS OF SOME ALGEBRAS ASSOCIATED WITH
 $\mathfrak {sl}_2$
$\mathfrak {sl}_2$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 747-778
- Print publication:
- December 2025
-
- Article
- Export citation
Superelliptic Affine Lie algebras and orthogonal polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e120
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth locus of twisted affine Schubert varieties and twisted affine Demazure modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wreath Macdonald operators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A bialgebra theory of Gel’fand-Dorfman algebras with applications to Lie conformal bialgebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 July 2025, pp. 1-33
-
- Article
- Export citation
INTEGRABLE MODULES OVER QUANTUM SYMMETRIC PAIR COIDEAL SUBALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 05 June 2025, pp. 2257-2282
- Print publication:
- November 2025
-
- Article
- Export citation
Gelfand–Tsetlin crystals
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 May 2025, pp. 1-14
-
- Article
- Export citation
 $\mathbf {5 \times 5}$-graded Lie algebras, cubic norm structures and quadrangular algebras
$\mathbf {5 \times 5}$-graded Lie algebras, cubic norm structures and quadrangular algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Formanek-Procesi group with base a right-angled Artin group: Lie algebra and residual nilpotence
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 13 May 2025, pp. 1-22
-
- Article
- Export citation
Diagrammatics for the smallest quantum coideal and Jones–Wenzl projectors
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 April 2025, pp. 1-20
-
- Article
- Export citation
A comparison between
 $SL_n$ spider categories
$SL_n$ spider categories
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant divisors and equivariant line bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 April 2025, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable homology of Lie algebras of derivations and homotopy invariants of wheeled operads
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 13 August 2025, pp. 756-799
- Print publication:
- April 2025
-
- Article
- Export citation
Corrigendum: Conformal blocks for Galois covers of algebraic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 15 August 2025, pp. 945-946
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation