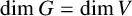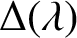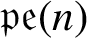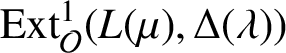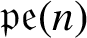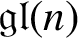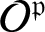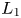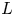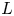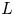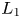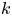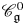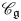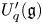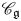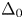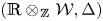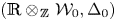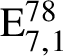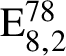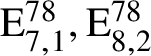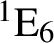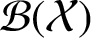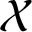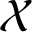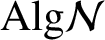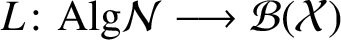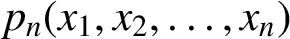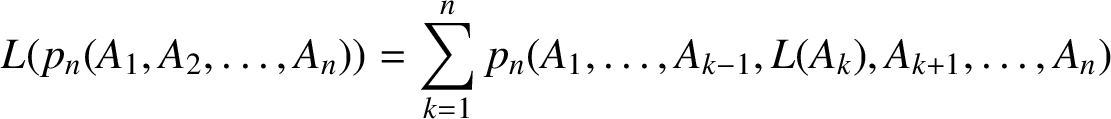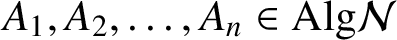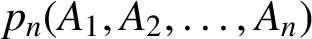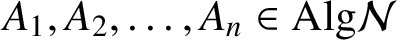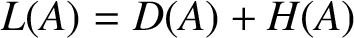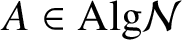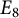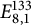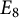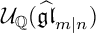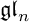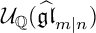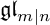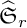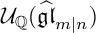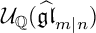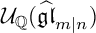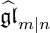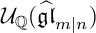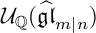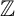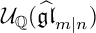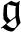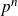Refine listing
Actions for selected content:
315 results in 17xxx
Proper Lie automorphisms of incidence algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 07 February 2022, pp. 702-715
- Print publication:
- September 2022
-
- Article
- Export citation
A NOTE ON ÉTALE REPRESENTATIONS FROM NILPOTENT ORBITS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 25 January 2022, pp. 113-125
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME HOMOLOGICAL PROPERTIES OF CATEGORY
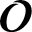 $\boldsymbol {\mathcal {O}}$ FOR LIE SUPERALGEBRAS
$\boldsymbol {\mathcal {O}}$ FOR LIE SUPERALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 21 January 2022, pp. 50-77
- Print publication:
- February 2023
-
- Article
- Export citation
A sandwich in thin lie algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 January 2022, pp. 136-145
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simply laced root systems arising from quantum affine algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 168-210
- Print publication:
- January 2022
-
- Article
- Export citation
The commutative nonassociative algebra of metric curvature tensors
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 09 December 2021, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Tits–Weiss conjecture and the Kneser–Tits conjecture for
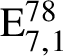 $\mathrm {E}^{78}_{7,1}$ and
$\mathrm {E}^{78}_{7,1}$ and 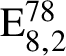 $\mathrm {E}^{78}_{8,2}$ (With an Appendix by R. M. Weiss)
$\mathrm {E}^{78}_{8,2}$ (With an Appendix by R. M. Weiss)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 23 November 2021, e75
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On free subalgebras of varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 22 November 2021, pp. 89-101
-
- Article
- Export citation
Wall-crossings and a categorification of K-theory stable bases of the Springer resolution
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2021, pp. 2341-2376
- Print publication:
- November 2021
-
- Article
- Export citation
Defining relations of quantum symmetric pair coideal subalgebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 05 October 2021, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unitary representations of type B rational Cherednik algebras and crystal combinatorics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 140-169
- Print publication:
- February 2023
-
- Article
- Export citation
LIE-TYPE DERIVATIONS OF NEST ALGEBRAS ON BANACH SPACES AND RELATED TOPICS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 29 September 2021, pp. 391-430
- Print publication:
- June 2022
-
- Article
- Export citation
The Allison–Faulkner construction of
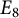 $E_8$
$E_8$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 September 2021, pp. 686-701
- Print publication:
- September 2022
-
- Article
- Export citation
A REALIZATION OF THE ENVELOPING SUPERALGEBRA
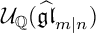 $ {\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
$ {\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 09 September 2021, pp. 516-551
- Print publication:
- September 2022
-
- Article
- Export citation
A generalization of the b-function lemma
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 07 September 2021, pp. 2199-2214
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wick polynomials in noncommutative probability: a group-theoretical approach
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 25 August 2021, pp. 1673-1699
- Print publication:
- December 2022
-
- Article
- Export citation
LIE ALGEBRA MODULES WHICH ARE LOCALLY FINITE AND WITH FINITE MULTIPLICITIES OVER THE SEMISIMPLE PART
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 02 August 2021, pp. 430-470
- Print publication:
- June 2022
-
- Article
- Export citation
Symmetry of Narayana Numbers and Rowvacuation of Root Posets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 July 2021, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mirabolic Satake equivalence and supergroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 22 July 2021, pp. 1724-1765
- Print publication:
- August 2021
-
- Article
- Export citation
The restricted Burnside problem for Moufang loops
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 201-211
- Print publication:
- July 2022
-
- Article
- Export citation