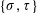 $\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter Operators, Infinitesimal Hom-bialgebras and the Associative (Bi)Hom-Yang–Baxter Equation
$\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter Operators, Infinitesimal Hom-bialgebras and the Associative (Bi)Hom-Yang–Baxter Equation
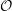 ${\mathcal{O}}$ for the Periplectic Lie Superalgebra
${\mathcal{O}}$ for the Periplectic Lie Superalgebra
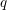 $q$-SCHUR SUPERALGEBRAS
$q$-SCHUR SUPERALGEBRAS