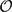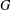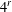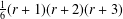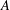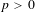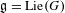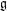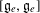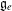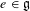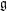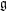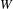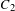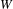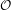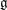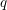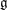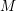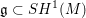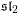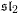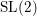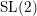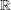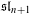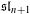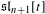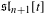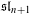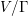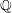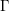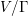Refine listing
Actions for selected content:
315 results in 17xxx
Generalized and degenerate Whittaker models
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 223-256
- Print publication:
- February 2017
-
- Article
- Export citation
SEMISIMPLICITY OF HECKE AND (WALLED) BRAUER ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 1-44
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
ON THE ALGEBRAIC PROPERTIES OF THE HUMAN ABO-BLOOD GROUP INHERITANCE PATTERN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 78-95
-
- Article
-
- You have access
- Export citation
Quivers with loops and generalized crystals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 10 / October 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 1999-2040
- Print publication:
- October 2016
-
- Article
- Export citation
W-ALGEBRAS FROM HEISENBERG CATEGORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 13 July 2016, pp. 981-1017
- Print publication:
- November 2018
-
- Article
- Export citation
On the minimal modules for exceptional Lie algebras: Jordan blocks and stabilizers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 235-258
-
- Article
-
- You have access
- Export citation
Finite Groups and Lie Rings with an Automorphism of Order 2n
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 15 June 2016, pp. 391-412
-
- Article
- Export citation
THE GROUP OF AUTOMORPHISMS OF THE LIE ALGEBRA OF DERIVATIONS OF A FIELD OF RATIONAL FUNCTIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 513-524
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
ON THE HOMOGENIZED ENVELOPING ALGEBRA OF THE LIE ALGEBRA Sℓ(2,ℂ) II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 189-219
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
ABELIAN IDEALS IN A COMPLEX SIMPLE LIE ALGEBRA
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 255-264
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
INTERCHANGE RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 310-334
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Application of Lie Algebra in Constructing Volume-Preserving Algorithms for Charged Particles Dynamics
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1397-1408
- Print publication:
- May 2016
-
- Article
- Export citation
RIGID ORBITS AND SHEETS IN REDUCTIVE LIE ALGEBRAS OVER FIELDS OF PRIME CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 04 April 2016, pp. 583-613
- Print publication:
- June 2018
-
- Article
- Export citation
JOSEPH IDEALS AND LISSE MINIMAL
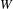 $W$ -ALGEBRAS
$W$ -ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 07 March 2016, pp. 397-417
- Print publication:
- April 2018
-
- Article
- Export citation
PERVERSE MOTIVES AND GRADED DERIVED CATEGORY
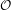 ${\mathcal{O}}$
${\mathcal{O}}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 26 February 2016, pp. 347-395
- Print publication:
- April 2018
-
- Article
- Export citation
Floer cohomology of
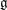 $\mathfrak{g}$-equivariant Lagrangian branes
$\mathfrak{g}$-equivariant Lagrangian branes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 December 2015, pp. 1071-1110
- Print publication:
- May 2016
-
- Article
- Export citation
Classification of horizontal
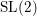 $\text{SL}(2)$s
$\text{SL}(2)$s
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 07 December 2015, pp. 918-954
- Print publication:
- May 2016
-
- Article
- Export citation
DEMAZURE MODULES OF LEVEL TWO AND PRIME REPRESENTATIONS OF QUANTUM AFFINE
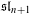 $\mathfrak{sl}_{n+1}$
$\mathfrak{sl}_{n+1}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 09 November 2015, pp. 75-105
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Counting resolutions of symplecticquotient singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 24 September 2015, pp. 99-114
- Print publication:
- January 2016
-
- Article
- Export citation
Quantum groups via cyclic quiver varieties I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 299-326
- Print publication:
- February 2016
-
- Article
- Export citation
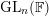

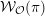
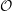
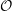
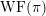
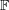
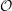
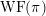
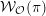
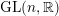
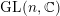

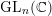
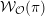
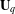
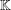
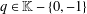
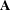
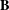
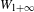
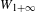
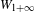
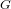
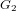
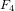
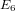
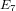

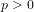

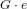
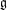

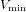
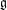
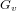
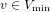
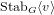
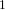
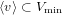
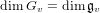
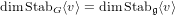
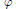 of order 2
of order 2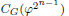 of the involution
of the involution 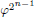 is nilpotent of class
is nilpotent of class 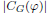 ) be the number of fixed points of
) be the number of fixed points of