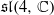Refine listing
Actions for selected content:
315 results in 17xxx
ON THE SUPPORT VARIETIES FOR DEMAZURE MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 19 March 2012, pp. 343-363
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
ON LEVI’S THEOREM FOR LEIBNIZ ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 184-185
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Slodowy slices and universal Poisson deformations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 121-144
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Mœglin’s theorem and Goldie rank polynomials in Cartan type A
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 09 November 2011, pp. 1741-1771
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation
THE GENERALIZED WITT MODULAR LIE SUPERALGEBRA OF CARTAN TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 18 November 2011, pp. 145-162
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
Cell 2-representations of finitary 2-categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 29 July 2011, pp. 1519-1545
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
ON ONE-DIMENSIONAL LEIBNIZ CENTRAL EXTENSIONS OF A FILIFORM LIE ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 29 July 2011, pp. 205-224
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
A NOTE ON DERIVATIONS OF LIE ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 21 July 2011, pp. 444-446
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Factorization of the canonical bases for higher-level Fock spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 20 June 2011, pp. 23-51
-
- Article
-
- You have access
- Export citation
IRREDUCIBLE REPRESENTATIONS OF THE HAMILTONIAN ALGEBRA H(2r;n)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 02 August 2011, pp. 403-430
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Gaudin subalgebras and stable rational curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 26 April 2011, pp. 1463-1478
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
The index complex of a maximal subalgebra of a Lie algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 08 April 2011, pp. 531-542
-
- Article
-
- You have access
- Export citation
Module structure on Lie powers and natural coalgebra-split sub-Hopf algebras of tensor algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 04 April 2011, pp. 467-504
-
- Article
-
- You have access
- Export citation
INDECOMPOSABLE REPRESENTATIONS OF THE EUCLIDEAN ALGEBRA 𝔢(3) FROM IRREDUCIBLE REPRESENTATIONS OF
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 01 April 2011, pp. 439-449
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Two generalizations of the PRV conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 18 March 2011, pp. 1321-1336
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
Is the function field of a reductive Lie algebra purely transcendental over the field of invariants for the adjoint action?
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 01 February 2011, pp. 428-466
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
ALTERNATING EULER SUMS AND SPECIAL VALUES OF THE WITTEN MULTIPLE ZETA FUNCTION ATTACHED TO

- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 18 February 2011, pp. 419-430
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
ON SUBGROUPS OF CLIFFORD GROUPS DEFINED BY JORDAN PAIRS OF RECTANGULAR MATRICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 21 October 2010, pp. 215-232
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Quasi-invariants of complex reflection groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 27 September 2010, pp. 965-1002
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
MAD SUBALGEBRAS AND LIE SUBALGEBRAS OF AN ENVELOPING ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 401-423
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
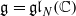 to give another proof of Mœglin’s theorem about completely prime primitive ideals in the enveloping algebra
to give another proof of Mœglin’s theorem about completely prime primitive ideals in the enveloping algebra 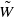 of Cartan type. We give a set of generators for
of Cartan type. We give a set of generators for  . Finally, we describe the homogeneous derivations of
. Finally, we describe the homogeneous derivations of 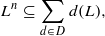
 and
and  . They correspond to
. They correspond to  and
and  -module structures. We establish that the transition matrices relating these two bases are unitriangular with coefficients in ℕ[
-module structures. We establish that the transition matrices relating these two bases are unitriangular with coefficients in ℕ[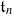 . We show that Gaudin subalgebras form a variety isomorphic to the moduli space
. We show that Gaudin subalgebras form a variety isomorphic to the moduli space 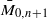 of stable curves of genus zero with
of stable curves of genus zero with 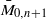 in a Grassmannian of (
in a Grassmannian of (