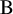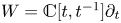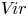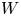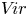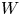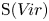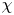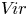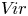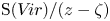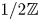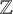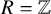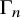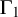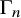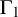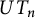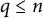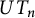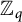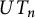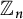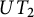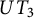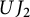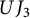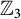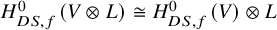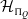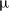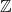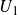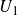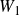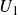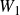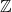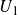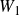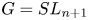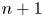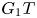Refine listing
Actions for selected content:
315 results in 17xxx
Comparison of quantizations of symmetric spaces: cyclotomic Knizhnik–Zamolodchikov equations and Letzter–Kolb coideals
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 May 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE QUANTUM ISOMERIC SUPERCATEGORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 25 April 2023, pp. 1077-1124
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Poisson spectrum of the symmetric algebra of the Virasoro algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 18 April 2023, pp. 933-984
- Print publication:
- May 2023
-
- Article
- Export citation
On the primality of totally ordered q-factorization graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 594-637
- Print publication:
- April 2024
-
- Article
- Export citation
Classification of simple Harish–Chandra modules over the Ovsienko–Roger superalgebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 14 March 2023, pp. 483-493
- Print publication:
- April 2024
-
- Article
- Export citation
Albert algebras over
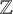 $\mathbb {Z}$ and other rings
$\mathbb {Z}$ and other rings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 March 2023, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Euler continuants in noncommutative quasi-Poisson geometry
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 October 2022, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Images of multilinear graded polynomials on upper triangular matrix algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 1540-1565
- Print publication:
- October 2023
-
- Article
- Export citation
CORRIGENDUM TO “CLUSTER CATEGORIES FROM GRASSMANNIANS AND ROOT COMBINATORICS”
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 269-273
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A categorical approach to dynamical quantum groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal order Abelian subgroups of Coxeter groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 02 August 2022, pp. 114-120
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Urod algebras and Translation of W-algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 08 June 2022, e33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hecke action on the principal block
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 19 July 2022, pp. 953-1019
- Print publication:
- May 2022
-
- Article
- Export citation
A boson-fermion correspondence in cohomological Donaldson–Thomas theory
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 11 April 2022, pp. S28-S52
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SHUFFLE ALGEBRAS FOR QUIVERS AND R-MATRICES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 22 March 2022, pp. 2583-2618
- Print publication:
- November 2023
-
- Article
- Export citation
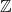 $\mathbb{Z}$-graded identities of the Lie algebras
$\mathbb{Z}$-graded identities of the Lie algebras 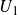 $U_1$ in characteristic 2
$U_1$ in characteristic 2
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 March 2022, pp. 49-58
- Print publication:
- January 2023
-
- Article
- Export citation
Symmetrisation and the Feigin–Frenkel centre
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 19 May 2022, pp. 585-622
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TAMARKIN–TSYGAN CALCULUS AND CHIRAL POISSON COHOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 751-765
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ACTIONS OF MONOIDAL CATEGORIES AND REPRESENTATIONS OF CARTAN TYPE LIE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 22 February 2022, pp. 2367-2402
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explicit calculations in an infinitesimal singular block of SLn
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 10 February 2022, pp. 19-52
-
- Article
- Export citation