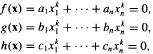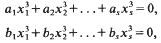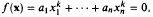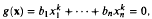Refine listing
Actions for selected content:
218 results in 11Dxx
Un nouveau critère pour l'équation de Catalan
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-73
- Print publication:
- December 2000
-
- Article
- Export citation
On integers with identical digits
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 411-417
- Print publication:
- December 1999
-
- Article
- Export citation
On some questions of Erdős and Graham about Egyptian fractions
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 359-372
- Print publication:
- December 1999
-
- Article
- Export citation
Simultaneous diagonal p–adic equations
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 337-349
- Print publication:
- December 1998
-
- Article
- Export citation
On simultaneous additive equations, IV
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 319-335
- Print publication:
- December 1998
-
- Article
- Export citation
Integer points on algebraic curves with exceptional units
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 145-164
- Print publication:
- October 1997
-
- Article
-
- You have access
- Export citation
Effective measures of irrationality for certain algebraic numbers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 329-344
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
Some Diophantine equations with almost all solutions trivial
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-36
- Print publication:
- June 1997
-
- Article
- Export citation
Cubic Diophantine inequalities
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 264-277
- Print publication:
- December 1995
-
- Article
- Export citation
On recursive solutions of a unit fraction equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 341-356
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
Three additive congruences to a large prime modulus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 3 / December 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 355-368
- Print publication:
- December 1993
-
- Article
-
- You have access
- Export citation
Simultaneous additive congruences to a large prime modulus
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
- Print publication:
- June 1992
-
- Article
- Export citation
On pairs of cubic Diophantine inequalities
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 250-263
- Print publication:
- December 1991
-
- Article
- Export citation
Small solutions of quadratic congruences, II
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 264-284
- Print publication:
- December 1991
-
- Article
- Export citation
On some diophantine problems involving powers and factorials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-7
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
Bounds for the solutions of some diophantine equations in terms of discriminants
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 8-26
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
Additive relations in fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 154-170
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
Pairs of additive congruences to a large prime modulus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 438-455
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation

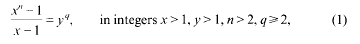
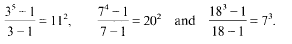
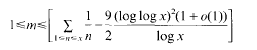
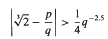 for any non-zero integers
for any non-zero integers 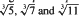 . Some Diophantine consequences are briefly discussed.
. Some Diophantine consequences are briefly discussed.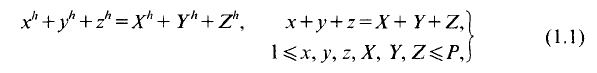
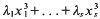
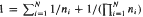 and discuss techniques for generating solutions. By examining a quadratic recurrence relation modulo a family of primes we have found some 500 new infinite sequences of solutions. We also initiate an investigation of the randomness of the distribution of solutions, and show that there are infinitely many solutions not generated by the aforementioned technique.
and discuss techniques for generating solutions. By examining a quadratic recurrence relation modulo a family of primes we have found some 500 new infinite sequences of solutions. We also initiate an investigation of the randomness of the distribution of solutions, and show that there are infinitely many solutions not generated by the aforementioned technique.