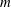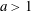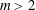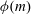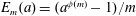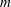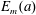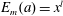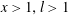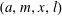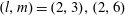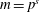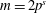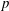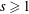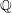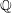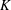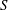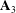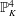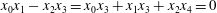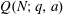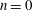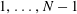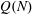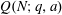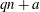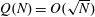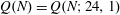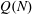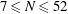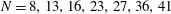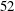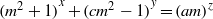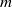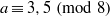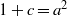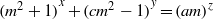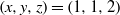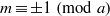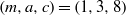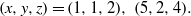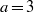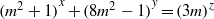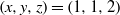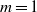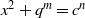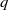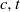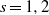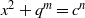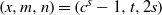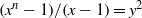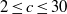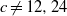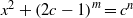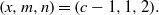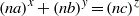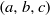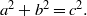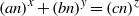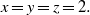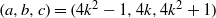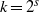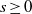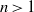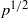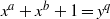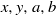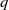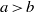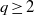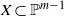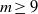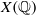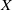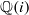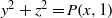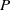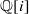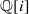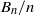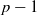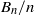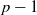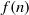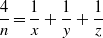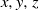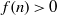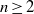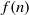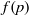Refine listing
Actions for selected content:
218 results in 11Dxx
Equivariant Compactifications of Two-Dimensional Algebraic Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 149-168
-
- Article
-
- You have access
- Export citation
ON EXPONENTIAL DIOPHANTINE EQUATIONS CONTAINING THE EULER QUOTIENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 11-18
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
The Hardy–Littlewood conjecture and rational points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 10 September 2014, pp. 2095-2111
- Print publication:
- December 2014
-
- Article
- Export citation
Counting imaginary quadratic points via universal torsors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 10 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 1631-1678
- Print publication:
- October 2014
-
- Article
- Export citation
On a conjecture of Rudin on squares in arithmetic progressions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 58-76
-
- Article
-
- You have access
- Export citation
ON THE EXPONENTIAL DIOPHANTINE EQUATION
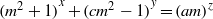 $\mathop{({m}^{2} + 1)}\nolimits ^{x} + \mathop{(c{m}^{2} - 1)}\nolimits ^{y} = \mathop{(am)}\nolimits ^{z} $
$\mathop{({m}^{2} + 1)}\nolimits ^{x} + \mathop{(c{m}^{2} - 1)}\nolimits ^{y} = \mathop{(am)}\nolimits ^{z} $
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 9-19
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
A NOTE ON THE DIOPHANTINE EQUATION
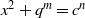 ${x}^{2} + {q}^{m} = {c}^{n} $
${x}^{2} + {q}^{m} = {c}^{n} $
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 26 November 2013, pp. 20-27
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
COUNTING RATIONAL POINTS ON CUBIC HYPERSURFACES: CORRIGENDUM
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 06 September 2013, pp. 101-107
- Print publication:
- January 2014
-
- Article
-
- You have access
- Export citation
A NOTE ON THE DIOPHANTINE EQUATION
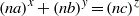 $\mathop{(na)}\nolimits ^{x} + \mathop{(nb)}\nolimits ^{y} = \mathop{(nc)}\nolimits ^{z} $
$\mathop{(na)}\nolimits ^{x} + \mathop{(nb)}\nolimits ^{y} = \mathop{(nc)}\nolimits ^{z} $
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 316-321
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
ON SOLUTIONS TO SOME POLYNOMIAL CONGRUENCES IN SMALL BOXES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 300-307
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
PERFECT POWERS WITH THREE DIGITS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 06 August 2013, pp. 66-84
- Print publication:
- January 2014
-
- Article
- Export citation
Rational points on singular intersections of quadrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 20 June 2013, pp. 1457-1494
- Print publication:
- September 2013
-
- Article
- Export citation
SOLUTIONS TO POLYNOMIAL CONGRUENCES IN WELL-SHAPED SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 12 June 2013, pp. 435-447
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Sur la conjecture de Manin pour certaines surfaces de Châtelet
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 759-819
- Print publication:
- October 2013
-
- Article
- Export citation
JEŚMANOWICZ’ CONJECTURE REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 15 February 2013, pp. 486-491
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
THE UNIVERSAL KUMMER CONGRUENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 106-132
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
COUNTING THE NUMBER OF SOLUTIONS TO THE ERDŐS–STRAUS EQUATION ON UNIT FRACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 15 May 2013, pp. 50-105
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
A DIOPHANTINE PROBLEM CONCERNING POLYGONAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 345-350
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Lifting, restricting and sifting integral points on affine homogeneous varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 1695-1716
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
APPROXIMATION OF AN ALGEBRAIC NUMBER BY PRODUCTS OF RATIONAL NUMBERS AND UNITS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2013, pp. 121-131
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
 on ℙ
on ℙ