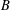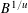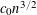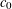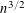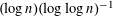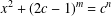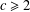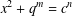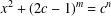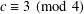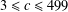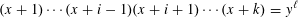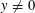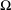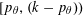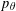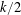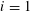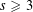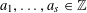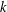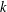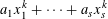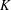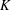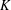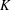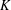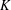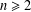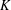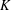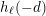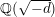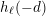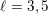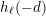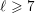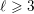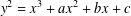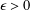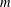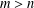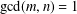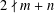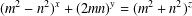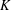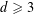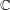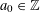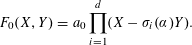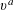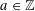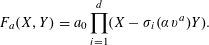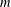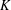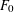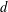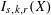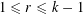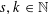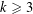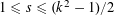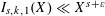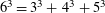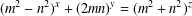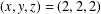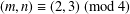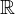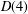Refine listing
Actions for selected content:
218 results in 11Dxx
SARNAK’S SATURATION PROBLEM FOR COMPLETE INTERSECTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 24 August 2018, pp. 1-56
- Print publication:
- 2019
-
- Article
- Export citation
A GENERALIZATION OF THE RAMANUJAN–NAGELL EQUATION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 22 August 2018, pp. 535-544
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
A NOTE ON THE DIOPHANTINE EQUATION
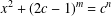 $x^{2}+(2c-1)^{m}=c^{n}$
$x^{2}+(2c-1)^{m}=c^{n}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 12 July 2018, pp. 188-195
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
BOUNDS FOR TRIPLE EXPONENTIAL SUMS WITH MIXED EXPONENTIAL AND LINEAR TERMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 64-69
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
VARIANTS OF ERDŐS–SELFRIDGE SUPERELLIPTIC CURVES AND THEIR RATIONAL POINTS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 380-386
- Print publication:
- 2018
-
- Article
- Export citation
THE DENSITY OF NUMBERS REPRESENTED BY DIAGONAL FORMS OF LARGE DEGREE
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 23 April 2018, pp. 542-550
- Print publication:
- 2018
-
- Article
- Export citation
ON PERFECT
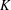 $K$ -RATIONAL CUBOIDS
$K$ -RATIONAL CUBOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 26-32
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Averages and moments associated to class numbers of imaginary quadratic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 2287-2309
- Print publication:
- November 2017
-
- Article
-
- You have access
- HTML
- Export citation
A NOTE ON SCHMIDT’S CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 09 June 2017, pp. 191-195
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
JEŚMANOWICZ’ CONJECTURE ON PYTHAGOREAN TRIPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 30-35
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
FAMILIES OF THUE EQUATIONS ASSOCIATED WITH A RANK ONE SUBGROUP OF THE UNIT GROUP OF A NUMBER FIELD
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1060-1080
- Print publication:
- 2017
-
- Article
- Export citation
VINOGRADOV SYSTEMS WITH A SLICE OFF
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 797-817
- Print publication:
- 2017
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PERFECT POWERS THAT ARE SUMS OF CONSECUTIVE CUBES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 05 October 2016, pp. 230-249
- Print publication:
- 2017
-
- Article
- Export citation
A NOTE ON JEŚMANOWICZ’ CONJECTURE CONCERNING PRIMITIVE PYTHAGOREAN TRIPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 5-13
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Effective Hasse principle for the intersection of two quadrics
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 73-82
-
- Article
-
- You have access
- Export citation
THE QUADRATIC FORM IN NINE PRIME VARIABLES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 223 / Issue 1 / September 2016
- Published online by Cambridge University Press:
- 18 August 2016, pp. 21-65
- Print publication:
- September 2016
-
- Article
-
- You have access
- HTML
- Export citation
AN UPPER BOUND FOR THE NUMBER OF DIOPHANTINE QUINTUPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 384-394
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
PERFECT POWERS IN PRODUCTS OF TERMS OF ELLIPTIC DIVISIBILITY SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 395-404
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
The genus, Frobenius number and pseudo-Frobenius numbers of numerical semigroups of type 2
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 1081-1090
- Print publication:
- October 2016
-
- Article
- Export citation
Rational points on Erdős–Selfridge superelliptic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 2249-2254
- Print publication:
- November 2016
-
- Article
- Export citation