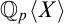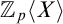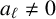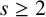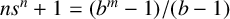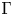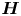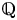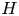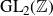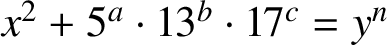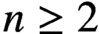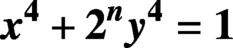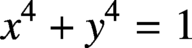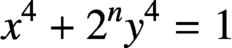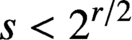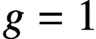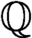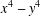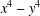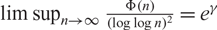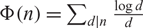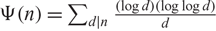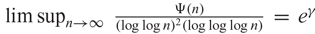Refine listing
Actions for selected content:
218 results in 11Dxx
Uniform Properties of Ideals in Rings of Restricted Power Series
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 June 2022, p. 258
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
Hensel minimality I
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 May 2022, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE INHOMOGENEOUS VINOGRADOV SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 396-403
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLVABILITY OF A SYSTEM OF POLYNOMIAL EQUATIONS MODULO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 23 March 2022, pp. 404-407
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIOPHANTINE EQUATIONS FOR POLYNOMIALS WITH RESTRICTED COEFFICIENTS, I (POWER VALUES)
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 22 February 2022, pp. 254-263
- Print publication:
- October 2022
-
- Article
- Export citation
ON REPUNIT CULLEN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 264-268
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Translates of homogeneous measures associated with observable subgroups on some homogeneous spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 22 December 2021, pp. 2657-2698
- Print publication:
- December 2021
-
- Article
- Export citation
COUNTEREXAMPLES TO THE HASSE PRINCIPLE IN FAMILIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 05 November 2021, pp. 18-27
- Print publication:
- August 2022
-
- Article
- Export citation
ON A PROBLEM OF RICHARD GUY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 12-18
- Print publication:
- February 2022
-
- Article
- Export citation
A UNIQUE PERFECT POWER DECAGONAL NUMBER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 06 August 2021, pp. 212-216
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A positive proportion of locally soluble quartic Thue equations are globally insoluble
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 05 August 2021, pp. 333-348
- Print publication:
- September 2022
-
- Article
- Export citation
SOLUTIONS TO A LEBESGUE–NAGELL EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 19-30
- Print publication:
- February 2022
-
- Article
- Export citation
Thue equations that simultaneously fail the Hasse principle
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 617-626
- Print publication:
- May 2022
-
- Article
- Export citation
On the Skolem problem and some related questions for parametric families of linear recurrence sequences
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2021, pp. 773-792
- Print publication:
- June 2022
-
- Article
- Export citation
NOTES ON THE K-RATIONAL DISTANCE PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 01 December 2020, pp. 40-44
- Print publication:
- August 2021
-
- Article
- Export citation
THE DIOPHANTINE EQUATION
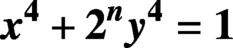 $\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS
$\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 06 November 2020, pp. 21-28
- Print publication:
- August 2021
-
- Article
- Export citation
A NOTE ON JEŚMANOWICZ’ CONJECTURE CONCERNING NONPRIMITIVE PYTHAGOREAN TRIPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 29-39
- Print publication:
- August 2021
-
- Article
- Export citation
THE EXPONENTIAL DIOPHANTINE PROBLEM FOR
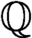 ${\mathbb {Q}}$
${\mathbb {Q}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 671-672
- Print publication:
- June 2020
-
- Article
- Export citation
INTEGERS REPRESENTED BY
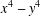 $x^{4}-y^{4}$ REVISITED
$x^{4}-y^{4}$ REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 38-49
- Print publication:
- February 2021
-
- Article
- Export citation
AN EXTENSION OF A RESULT OF ERDŐS AND ZAREMBA
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 13 May 2020, pp. 193-222
-
- Article
-
- You have access
- Export citation