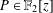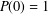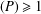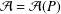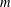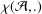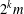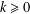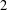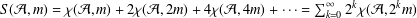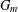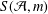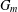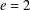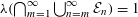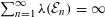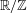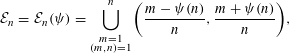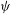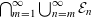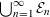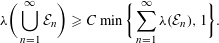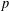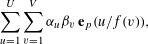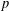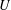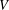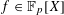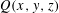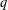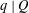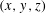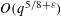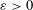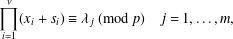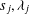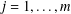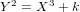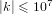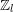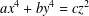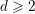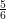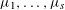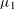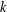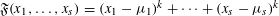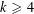Refine listing
Actions for selected content:
218 results in 11Dxx
On Systems of Complexity One in the Primes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 May 2016, pp. 133-163
-
- Article
- Export citation
Numerical semigroups with a given set of pseudo-Frobenius numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 186-205
-
- Article
-
- You have access
- Export citation
SETS WITH EVEN PARTITION FUNCTIONS AND CYCLOTOMIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 14 March 2016, pp. 289-302
-
- Article
-
- You have access
- Export citation
Minor arcs, mean values, and restriction theory for exponential sums over smooth numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 23 February 2016, pp. 1121-1158
- Print publication:
- June 2016
-
- Article
- Export citation
Rational points on linear slices of diagonal hypersurfaces
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 51-100
-
- Article
-
- You have access
- Export citation
RATIONAL POINTS ON CUBIC HYPERSURFACES THAT SPLIT INTO FOUR FORMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 29 January 2016, pp. 430-440
- Print publication:
- 2016
-
- Article
- Export citation
THE DUFFIN–SCHAEFFER-TYPE CONJECTURES IN VARIOUS LOCAL FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 06 May 2016, pp. 753-800
- Print publication:
- 2016
-
- Article
- Export citation
ON BILINEAR EXPONENTIAL AND CHARACTER SUMS WITH RECIPROCALS OF POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 842-859
- Print publication:
- 2016
-
- Article
- Export citation
SMALL SOLUTIONS OF QUADRATIC CONGRUENCES, AND CHARACTER SUMS WITH BINARY QUADRATIC FORMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 18 February 2016, pp. 551-571
- Print publication:
- 2016
-
- Article
- Export citation
SYSTEMS OF CONGRUENCES WITH PRODUCTS OF VARIABLES FROM SHORT INTERVALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 364-371
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
ON THE SQUARE-FREE REPRESENTATION FUNCTION OF A NORM FORM AND NILSEQUENCES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 11 November 2015, pp. 107-135
- Print publication:
- February 2018
-
- Article
- Export citation
Mordell’s equation: a classical approach
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 September 2015, pp. 633-646
-
- Article
-
- You have access
- Export citation
NON-ARCHIMEDEAN YOMDIN–GROMOV PARAMETRIZATIONS AND POINTS OF BOUNDED HEIGHT
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 14 August 2015, e5
-
- Article
-
- You have access
- Open access
- Export citation
Growth of
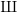 $\unicode[STIX]{x0428}$ in towers for isogenous curves
$\unicode[STIX]{x0428}$ in towers for isogenous curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 30 June 2015, pp. 1981-2005
- Print publication:
- November 2015
-
- Article
- Export citation
SOME QUARTIC DIOPHANTINE EQUATIONS IN THE GAUSSIAN INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 187-194
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Mutations of Fake Weighted Projective Planes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 10 June 2015, pp. 271-285
-
- Article
- Export citation
Pairs of quadrics in 11 variables
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 23 March 2015, pp. 1189-1214
- Print publication:
- July 2015
-
- Article
- Export citation
The asymptotic Fermat’s Last Theorem for five-sixths of real quadratic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 8 / August 2015
- Published online by Cambridge University Press:
- 06 March 2015, pp. 1395-1415
- Print publication:
- August 2015
-
- Article
- Export citation
WARING’S PROBLEM WITH SHIFTS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 06 March 2015, pp. 13-46
- Print publication:
- 2016
-
- Article
- Export citation
Effective limit distribution of the Frobenius numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 898-916
- Print publication:
- May 2015
-
- Article
- Export citation