Refine listing
Actions for selected content:
218 results in 11Dxx
Diagonal quartic surfaces and transcendental elements of the Brauer group
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 28 May 2010, pp. 769-798
- Print publication:
- October 2010
-
- Article
- Export citation
A NOTE ON SIMULTANEOUS CONGRUENCES, II: MORDELL REVISED
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 25 March 2010, pp. 261-275
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Rational points on cubic hypersurfaces that split off a form. With an appendix by J.-L. Colliot-Thélène
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 15 February 2010, pp. 853-885
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
Zeros of systems of 𝔭-adic quadratic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 271-287
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF SOLUTIONS OF THE DIOPHANTINE EQUATION axm−byn=c
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 13 January 2010, pp. 177-185
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
ON m-COVERS AND m-SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 05 October 2009, pp. 223-235
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
On quadratic fields generated by the Shanks sequence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 719-729
-
- Article
-
- You have access
- Export citation
ON THE CONJECTURE OF JEŚMANOWICZ CONCERNING PYTHAGOREAN TRIPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 July 2009, pp. 413-422
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Perfect powers from products of consecutive terms in arithmetic progression
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 845-864
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
Brauer–Manin obstruction for integral points of homogeneous spaces and representation by integral quadratic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 309-363
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
A problem of Ozanam
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 37-44
-
- Article
-
- You have access
- Export citation
Binary linear forms as sums of two squares
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1375-1402
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF REPRESENTATIONS OF INTEGERS BY CERTAIN QUADRATIC FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 129-140
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
MODULAR DIOPHANTINE INEQUALITIES AND ROTATIONS OF NUMERICAL SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 315-328
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
On systems of diagonal forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 221-236
- Print publication:
- April 2007
-
- Article
-
- You have access
- Export citation
Rational points on the superelliptic Erdös Selfridge curve of fifth degree
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-124
- Print publication:
- December 2003
-
- Article
- Export citation
On integers which are not differences of two powers
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-243
- Print publication:
- June 2002
-
- Article
- Export citation
On shifted products which are powers
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 227-230
- Print publication:
- June 2002
-
- Article
- Export citation
On simultaneous diagonal inequalities, II
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 191-202
- Print publication:
- December 2001
-
- Article
- Export citation
Asymptotic lower bounds for Diophantine inequalities
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-159
- Print publication:
- December 2000
-
- Article
- Export citation

 subsets
subsets 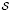 -unit equations as well as bounds for character sums to obtain a lower bound on the number of distinct fields among
-unit equations as well as bounds for character sums to obtain a lower bound on the number of distinct fields among 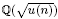 for
for 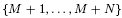 . Fields of this type include the Shanks fields and their generalizations.
. Fields of this type include the Shanks fields and their generalizations.