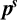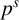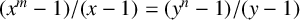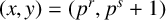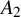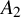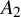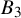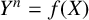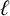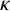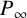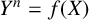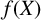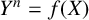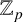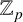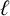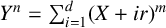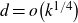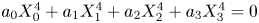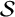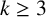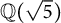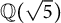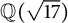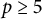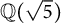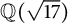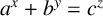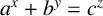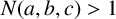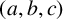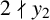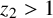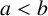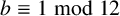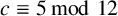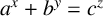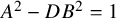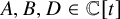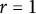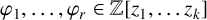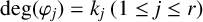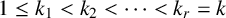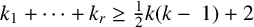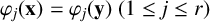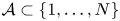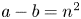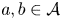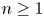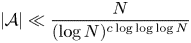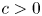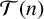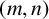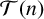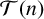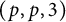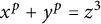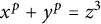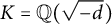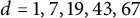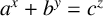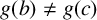Refine listing
Actions for selected content:
218 results in 11Dxx
Galois groups and prime divisors in random quadratic sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 07 September 2023, pp. 95-122
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weil Sums over Small Subgroups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 39-53
- Print publication:
- January 2024
-
- Article
- Export citation
GHOSTS AND CONGRUENCES FOR
 $\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
$\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 02 August 2023, pp. 96-127
- Print publication:
- February 2024
-
- Article
- Export citation
A NOTE ON THE GOORMAGHTIGH EQUATION CONCERNING DIFFERENCE SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 443-452
- Print publication:
- June 2024
-
- Article
- Export citation
q-deformed rational numbers and the 2-Calabi–Yau category of type
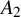 $A_{2}$
$A_{2}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 June 2023, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIOPHANTINE EQUATIONS OF THE FORM
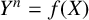 $Y^n=f(X)$ OVER FUNCTION FIELDS
$Y^n=f(X)$ OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 18 May 2023, pp. 379-390
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THEOREMS OF LEGENDRE TYPE FOR OVERPARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 28 April 2023, pp. 265-275
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Paucity problems and some relatives of Vinogradov’s mean value theorem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 05 April 2023, pp. 327-343
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Diagonal quartic surfaces with a Brauer–Manin obstruction
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 17 March 2023, pp. 659-710
- Print publication:
- April 2023
-
- Article
- Export citation
WHEN IS A NUMERICAL SEMIGROUP A QUOTIENT?
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 67-76
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fermat’s Last Theorem over
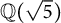 $\mathbb {Q}(\sqrt {\text{5}})$ and
$\mathbb {Q}(\sqrt {\text{5}})$ and 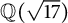 $\mathbb {Q}(\sqrt {\text{17}})$
$\mathbb {Q}(\sqrt {\text{17}})$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 November 2022, pp. 18-38
- Print publication:
- February 2024
-
- Article
- Export citation
ON A CONJECTURE CONCERNING THE NUMBER OF SOLUTIONS TO
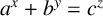 $a^x+b^y=c^z$
$a^x+b^y=c^z$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 40-49
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTEGRAL POINTS ON SINGULAR DEL PEZZO SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 10 November 2022, pp. 1259-1294
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Betti maps, Pell equations in polynomials and almost-Belyi maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 October 2022, e84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
D-finite multivariate series with arithmetic restrictions on their coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1745-1779
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PAUCITY PROBLEM FOR CERTAIN SYMMETRIC DIOPHANTINE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 29-39
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new upper bound for sets with no square differences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 30 September 2022, pp. 1777-1798
- Print publication:
- August 2022
-
- Article
- Export citation
TIGHT UNIVERSAL SUMS OF m-GONAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 40-52
- Print publication:
- February 2023
-
- Article
- Export citation
On ternary Diophantine equations of signature
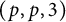 $(p,p,\text{3})$ over number fields
$(p,p,\text{3})$ over number fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 1293-1313
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE NUMBER OF SOLUTIONS OF TERNARY PURELY EXPONENTIAL DIOPHANTINE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 June 2022, pp. 53-65
- Print publication:
- February 2023
-
- Article
- Export citation