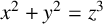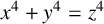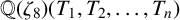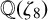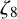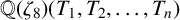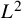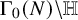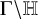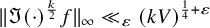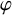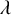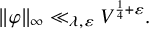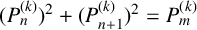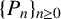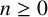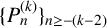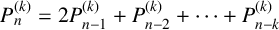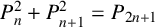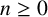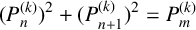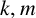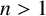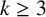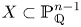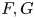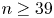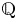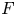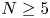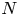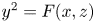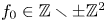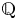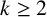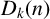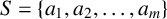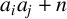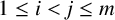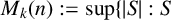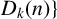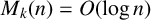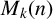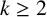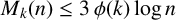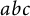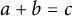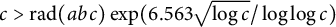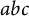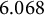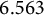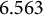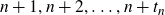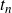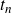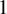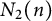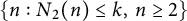Refine listing
Actions for selected content:
218 results in 11Dxx
Arithmetic Ramsey theory over the primes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1-47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FROBENIUS NUMBERS ASSOCIATED WITH DIOPHANTINE TRIPLES OF
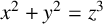 $x^2+y^2=z^3$
$x^2+y^2=z^3$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 57-66
- Print publication:
- August 2025
-
- Article
- Export citation
POINTS ON
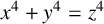 $x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF
$x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF 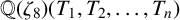 ${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 November 2024, pp. 19-31
- Print publication:
- February 2025
-
- Article
- Export citation
IMPROVED UPPER BOUNDS ON DIOPHANTINE TUPLES WITH THE PROPERTY
 $D(n)$
$D(n)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 428-432
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A MORDELL–LANG-TYPE PROBLEM FOR
 $\mathrm{GL}_{m}$
$\mathrm{GL}_{m}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 433-444
- Print publication:
- June 2025
-
- Article
- Export citation
Theta functions, fourth moments of eigenforms and the sup-norm problem II
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISED QUADRATIC FORMS OVER TOTALLY REAL NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 2859-2912
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unit fractions with shifted prime denominators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 02 April 2024, pp. 2285-2295
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How to solve a binary cubic equation in integers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 609-624
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DIOPHANTINE EQUATION
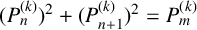 $(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
$(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 211-215
- Print publication:
- October 2024
-
- Article
- Export citation
On the Hasse principle for complete intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 771-835
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERATING FUNCTIONS FOR THE QUOTIENTS OF NUMERICAL SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. 427-438
- Print publication:
- December 2024
-
- Article
- Export citation
Most odd-degree binary forms fail to primitively represent a square
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 481-517
- Print publication:
- March 2024
-
- Article
- Export citation
The Manin–Peyre conjecture for smooth spherical Fano varieties of semisimple rank one
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 January 2024, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EFFECTIVE BOUND FOR GENERALISED DIOPHANTINE m-TUPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 242-253
- Print publication:
- April 2024
-
- Article
- Export citation
A new lower bound in the
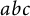 $abc$ conjecture
$abc$ conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 369-378
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A problem of Erdős–Graham–Granville–Selfridge on integral points on hyperelliptic curves
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 05 October 2023, pp. 309-323
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hensel minimality II: Mixed characteristic and a diophantine application
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete restriction estimates for forms in many variables
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 923-939
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equal-Sum-Product problem II
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 13 September 2023, pp. 582-592
- Print publication:
- September 2024
-
- Article
- Export citation