Refine listing
Actions for selected content:
230 results in 11Mxx
On the non-homogeneous quadratic Bessel zeta function
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 123-130
- Print publication:
- December 2004
-
- Article
- Export citation
A simple remark on Dirichlet series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-4
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Character sums and the series L(1, χ)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-436
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
The behaviour of the Riemann zeta-function on the critical line
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 281-313
- Print publication:
- December 1999
-
- Article
- Export citation
Hardy's legacy to number theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 238-266
- Print publication:
- October 1998
-
- Article
-
- You have access
- Export citation
On the eigenvalues of Redheffer's matrix, II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 2 / April 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 260-273
- Print publication:
- April 1996
-
- Article
-
- You have access
- Export citation
Mean-values of the Riemann zeta-function
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 158-174
- Print publication:
- June 1995
-
- Article
- Export citation
The large values of the Riemann Zeta-function
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 203-214
- Print publication:
- December 1993
-
- Article
- Export citation
Long mollifiers of the Riemann Zeta-function
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-87
- Print publication:
- June 1993
-
- Article
- Export citation
Uniform distribution and lattice point counting
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 39-50
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
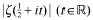 between successive zeros. Our results are to be independent of any unproved hypothesis. Put
between successive zeros. Our results are to be independent of any unproved hypothesis. Put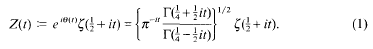
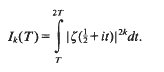
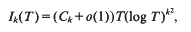
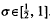 . By refining Selberg's method, we study the large values of
. By refining Selberg's method, we study the large values of 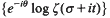 as
as 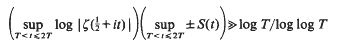
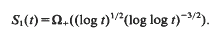
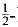 -line, where
-line, where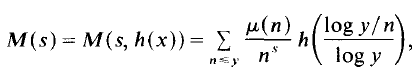
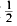 yields κ > 0·3562, having 0 < θ <
yields κ > 0·3562, having 0 < θ < 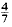 gives κ > 0·40219, and it is necessary to have θ > 0·165 in order to obtain a positive lower bound for κ. At present, it is known that the asymptotic formula remains valid for 0 < θ <
gives κ > 0·40219, and it is necessary to have θ > 0·165 in order to obtain a positive lower bound for κ. At present, it is known that the asymptotic formula remains valid for 0 < θ < 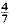 , this is due to Conrey. Without assuming the Riemann Hypothesis, Levinson's method provides the only known way of obtaining a positive lower bound for κ.
, this is due to Conrey. Without assuming the Riemann Hypothesis, Levinson's method provides the only known way of obtaining a positive lower bound for κ.