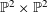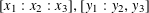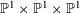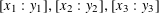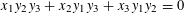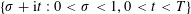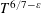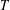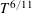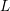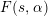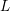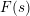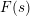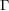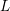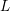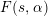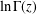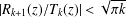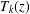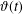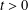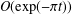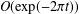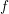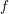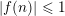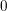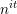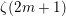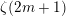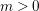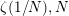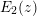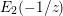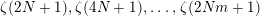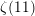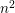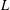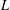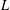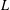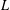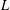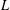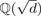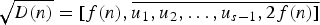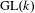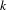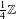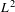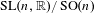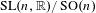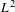Refine listing
Actions for selected content:
230 results in 11Mxx
THE POWER-SAVING MANIN–PEYRE CONJECTURE FOR A SENARY CUBIC
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 22 May 2019, pp. 789-830
- Print publication:
- 2019
-
- Article
- Export citation
ON SIMPLE ZEROS OF THE DEDEKIND ZETA-FUNCTION OF A QUADRATIC NUMBER FIELD
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 22 May 2019, pp. 851-861
- Print publication:
- 2019
-
- Article
- Export citation
Mean values of derivatives of L-functions in function fields: III
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 905-913
- Print publication:
- August 2019
-
- Article
- Export citation
ANALOGUES OF THE AOKI–OHNO AND LE–MURAKAMI RELATIONS FOR FINITE MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 34-40
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
ON THE STANDARD TWIST OF THE
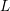 $L$-FUNCTIONS OF HALF-INTEGRAL WEIGHT CUSP FORMS
$L$-FUNCTIONS OF HALF-INTEGRAL WEIGHT CUSP FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 150-180
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
ON THE ACCURACY OF ASYMPTOTIC APPROXIMATIONS TO THE LOG-GAMMA AND RIEMANN–SIEGEL THETA FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 319-337
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Approximating the Riemann Zeta-function by Polynomials with Restricted Zeros
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 475-478
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
A new proof of Halász’s theorem, and its consequences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 126-163
- Print publication:
- January 2019
-
- Article
- Export citation
BEYOND ENDOSCOPY VIA THE TRACE FORMULA – IIITHE STANDARD REPRESENTATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 12 November 2018, pp. 1349-1387
- Print publication:
- July 2020
-
- Article
- Export citation
Cyclotomic analogues of finite multiple zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 06 November 2018, pp. 2701-2721
- Print publication:
- December 2018
-
- Article
- Export citation
GENERALIZED LAMBERT SERIES, RAABE’S COSINE TRANSFORM AND A GENERALIZATION OF RAMANUJAN’S FORMULA FOR
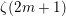 $\unicode[STIX]{x1D701}(2m+1)$
$\unicode[STIX]{x1D701}(2m+1)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 04 October 2018, pp. 232-293
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
THE RECIPROCITY LAW FOR THE TWISTED SECOND MOMENT OF DIRICHLET
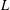 $L$ -FUNCTIONS OVER RATIONAL FUNCTION FIELDS
$L$ -FUNCTIONS OVER RATIONAL FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 28 August 2018, pp. 383-388
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
GOLDBACH REPRESENTATIONS IN ARITHMETIC PROGRESSIONS AND ZEROS OF DIRICHLET L-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 24 August 2018, pp. 57-97
- Print publication:
- 2019
-
- Article
- Export citation
Distribution of Class Numbers in Continued Fraction Families of Real Quadratic Fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 20 August 2018, pp. 1193-1212
-
- Article
- Export citation
ON THE ABSENCE OF ZEROS IN INFINITE ARITHMETIC PROGRESSION FORCERTAIN ZETA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 376-382
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
SOME HYPERGEOMETRIC INTEGRALS FOR LINEAR FORMS IN ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 372-375
- Print publication:
- December 2018
-
- Article
-
- You have access
- Open access
- Export citation
SHIDLOVSKY’S MULTIPLICITY ESTIMATE AND IRRATIONALITY OF ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 145-172
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
On the zeros of Dirichlet
 $L$ -functions
$L$ -functions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 May 2018, pp. 140-154
-
- Article
-
- You have access
- Export citation
EPSTEIN ZETA-FUNCTIONS, SUBCONVEXITY, AND THE PURITY CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 02 April 2018, pp. 581-596
- Print publication:
- March 2020
-
- Article
- Export citation
APPROXIMATION OF
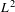 $L^{2}$-ANALYTIC TORSION FOR ARITHMETIC QUOTIENTS OF THE SYMMETRIC SPACE
$L^{2}$-ANALYTIC TORSION FOR ARITHMETIC QUOTIENTS OF THE SYMMETRIC SPACE 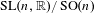 $\operatorname{SL}(n,\mathbb{R})/\operatorname{SO}(n)$
$\operatorname{SL}(n,\mathbb{R})/\operatorname{SO}(n)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 14 February 2018, pp. 307-350
- Print publication:
- March 2020
-
- Article
- Export citation