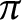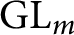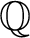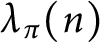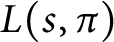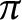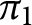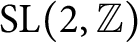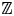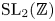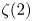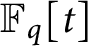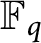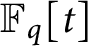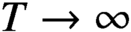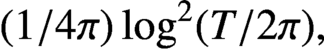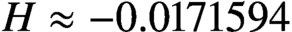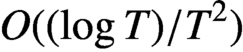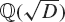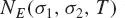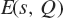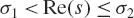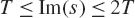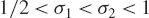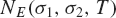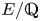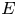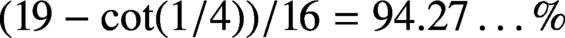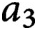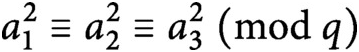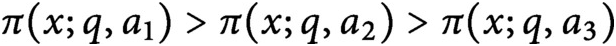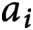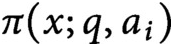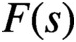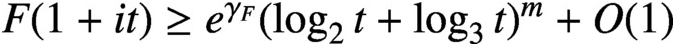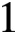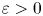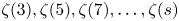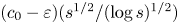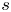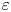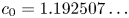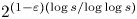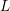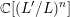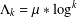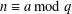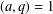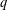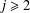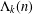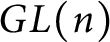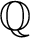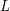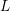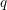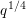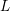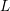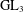Refine listing
Actions for selected content:
230 results in 11Mxx
Cancellation of two classes of dirichlet coefficients over Beatty sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 234-252
- Print publication:
- March 2022
-
- Article
- Export citation
ON A WEIGHTED SUM OF MULTIPLE $\mathbf{{T}}$
 -VALUES OF FIXED WEIGHT AND DEPTH
-VALUES OF FIXED WEIGHT AND DEPTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 398-405
- Print publication:
- December 2021
-
- Article
- Export citation
Depth-graded motivic multiple zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 22 March 2021, pp. 529-572
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vanishing of multizeta values over
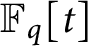 $\mathbb {F}_q[t]$ at negative integers
$\mathbb {F}_q[t]$ at negative integers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 9-29
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- Export citation
The second moment of symmetric square L-functions over Gaussian integers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 January 2021, pp. 54-80
- Print publication:
- February 2022
-
- Article
- Export citation
A HARMONIC SUM OVER NONTRIVIAL ZEROS OF THE RIEMANN ZETA-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 20 November 2020, pp. 59-65
- Print publication:
- August 2021
-
- Article
- Export citation
Zeros of the Epstein zeta function to the right of the critical line
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 17 November 2020, pp. 265-276
- Print publication:
- September 2021
-
- Article
- Export citation
Erratum: Limiting properties of the distribution of primes in an arbitrarily large number of residue classes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 1041-1044
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
Non-vanishing of class group L-functions for number fields with a small regulator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2423-2436
- Print publication:
- November 2020
-
- Article
- Export citation
ONE-LEVEL DENSITY OF LOW-LYING ZEROS OF QUADRATIC HECKE L-FUNCTIONS OF IMAGINARY QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 29 October 2020, pp. 170-192
- Print publication:
- April 2022
-
- Article
- Export citation
Densities in certain three-way prime number races
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 October 2020, pp. 232-265
- Print publication:
- February 2022
-
- Article
- Export citation
LARGE VALUES OF L-FUNCTIONS ON THE 1-LINE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 October 2020, pp. 230-243
- Print publication:
- April 2021
-
- Article
- Export citation
A note on the number of irrational odd zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 09 October 2020, pp. 1699-1717
- Print publication:
- August 2020
-
- Article
- Export citation
ANALYTIC PROPERTIES OF EISENSTEIN SERIES AND STANDARD
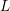 $L$ -FUNCTIONS
$L$ -FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 168-203
- Print publication:
- December 2021
-
- Article
- Export citation
UNEXPECTED AVERAGE VALUES OF GENERALIZED VON MANGOLDT FUNCTIONS IN RESIDUE CLASSES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 127-144
- Print publication:
- August 2021
-
- Article
- Export citation
Large values of Dirichlet L-functions at zeros of a class of L-functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 01 July 2020, pp. 1459-1505
- Print publication:
- December 2021
-
- Article
- Export citation
A CLASS OF NONHOLOMORPHIC MODULAR FORMS II: EQUIVARIANT ITERATED EISENSTEIN INTEGRALS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 28 May 2020, e31
-
- Article
-
- You have access
- Open access
- Export citation
Motohashi’s fourth moment identity for non-archimedean test functions and applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 April 2020, pp. 1004-1038
- Print publication:
- May 2020
-
- Article
- Export citation
THE DE BRUIJN–NEWMAN CONSTANT IS NON-NEGATIVE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 April 2020, e6
-
- Article
-
- You have access
- Open access
- Export citation
PERIODIC TWISTS OF
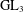 $\operatorname{GL}_{3}$-AUTOMORPHIC FORMS
$\operatorname{GL}_{3}$-AUTOMORPHIC FORMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 12 March 2020, e15
-
- Article
-
- You have access
- Open access
- Export citation