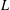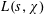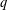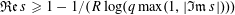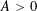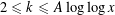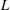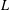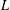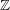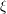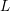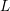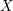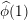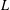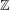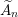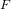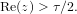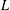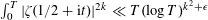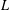Refine listing
Actions for selected content:
230 results in 11Mxx
EXPLICIT ZERO-FREE REGIONS FOR DIRICHLET
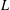 $L$ -FUNCTIONS
$L$ -FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 445-474
- Print publication:
- 2018
-
- Article
- Export citation
LARGE BIAS FOR INTEGERS WITH PRIME FACTORS IN ARITHMETIC PROGRESSIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 237-252
- Print publication:
- 2018
-
- Article
- Export citation
TRANSCENDENTAL SUMS RELATED TO THE ZEROS OF ZETA FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 875-897
- Print publication:
- 2018
-
- Article
- Export citation
TRUNCATED PRODUCT REPRESENTATIONS FOR
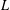 $L$ -FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE
$L$ -FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 06 February 2018, pp. 137-158
- Print publication:
- 2018
-
- Article
- Export citation
Odd zeta motive and linear forms in odd zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 342-379
- Print publication:
- February 2018
-
- Article
- Export citation
INTERPOLATED SCHUR MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 25 October 2017, pp. 289-307
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
MULTI-POLY-BERNOULLI NUMBERS AND RELATED ZETA FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 19-54
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
THE DOUBLE SHUFFLE RELATIONS FOR MULTIPLE EISENSTEIN SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 180-212
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
On the fourth moment of Hecke–Maass forms and the random wave conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1479-1511
- Print publication:
- July 2017
-
- Article
- Export citation
Low-lying zeros of quadratic Dirichlet
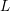 $L$ -functions: lower order terms for extended support
$L$ -functions: lower order terms for extended support
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 1196-1216
- Print publication:
- June 2017
-
- Article
- Export citation
ON ALGEBRAIC DIFFERENTIAL EQUATIONS FOR THE GAMMA FUNCTION AND
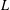 $L$ -FUNCTIONS IN THE EXTENDED SELBERG CLASS
$L$ -FUNCTIONS IN THE EXTENDED SELBERG CLASS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 36-43
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
EXPLICIT ZERO-COUNTING THEOREM FOR HECKE–LANDAU ZETA-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 400-411
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
ZETA ELEMENTS IN DEPTH 3 AND THE FUNDAMENTAL LIE ALGEBRA OF THE INFINITESIMAL TATE CURVE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 05 January 2017, e1
-
- Article
-
- You have access
- Open access
- Export citation
ON MULTIPLICATIVE COMPOSITIONS OF INTEGERS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1081-1090
- Print publication:
- 2017
-
- Article
- Export citation
SPECTRAL ZETA FUNCTIONS FOR THE QUANTUM RABI MODELS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 01 December 2016, pp. 52-98
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
Affine Weyl group multiple Dirichlet series: type
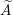 $\widetilde{A}$
$\widetilde{A}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 08 November 2016, pp. 2503-2523
- Print publication:
- December 2016
-
- Article
- Export citation
REMARKS ON THE MIXED JOINT UNIVERSALITY FOR A CLASS OF ZETA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 187-198
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
On a Li-type criterion for zero-free regions of certain Dirichlet series with real coefficients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 October 2016, pp. 259-280
-
- Article
-
- You have access
- Export citation
SHIFTED MOMENTS OF
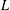 $L$ -FUNCTIONS ANDMOMENTS OF THETA FUNCTIONS
$L$ -FUNCTIONS ANDMOMENTS OF THETA FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 27 September 2016, pp. 196-212
- Print publication:
- 2017
-
- Article
- Export citation
RAMANUJAN CAYLEY GRAPHS OF FROBENIUS GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 26 September 2016, pp. 373-383
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation