Refine listing
Actions for selected content:
230 results in 11Mxx
RATIONAL APPROXIMATIONS TO VALUES OF BELL POLYNOMIALS AT POINTS INVOLVING EULER’S CONSTANT AND ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2012, pp. 71-98
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
ON A CERTAIN CONVOLUTION OF POLYLOGARITHMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 07 February 2012, pp. 461-472
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
ALTERNATING EULER SUMS AND SPECIAL VALUES OF THE WITTEN MULTIPLE ZETA FUNCTION ATTACHED TO

- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 18 February 2011, pp. 419-430
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
A NOTE ON SPECIAL VALUES OF CERTAIN DIRICHLET L-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 13 October 2010, pp. 435-438
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
One level density of low-lying zeros of families of L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 07 September 2010, pp. 1-18
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Subconvexity for a double Dirichlet series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 07 September 2010, pp. 355-374
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
A DETERMINANT FORMULA FOR RELATIVE CONGRUENCE ZETA FUNCTIONS FOR CYCLOTOMIC FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 15 July 2010, pp. 133-144
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
On mean values and non-vanishing of derivatives of L-functions in a nonlinear family
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 20 April 2010, pp. 19-34
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
A NOTE ON THE SECOND MOMENT OF AUTOMORPHIC L-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 35-44
- Print publication:
- January 2010
-
- Article
- Export citation
Produit eulérien motivique et courbes rationnelles sur les variétés toriques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1360-1400
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
The convergence of Euler products over p-adic number fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 583-606
-
- Article
-
- You have access
- Export citation
Subconvexity bounds for automorphic L-functions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 23 July 2009, pp. 95-124
- Print publication:
- January 2010
-
- Article
- Export citation
EVALUATION OF CERTAIN CLASSES OF EISENSTEIN-TYPE SERIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 239-247
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
p-units in ray class fields of real quadratic number fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 364-392
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
ON SOME WEIGHTED AVERAGE VALUES OF L-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 26 February 2009, pp. 183-186
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Integral moments of automorphic L-functions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 16 October 2008, pp. 335-382
- Print publication:
- April 2009
-
- Article
- Export citation
A JOINT UNIVERSALITY THEOREM FOR PERIODIC HURWITZ ZETA-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 13-33
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
A Discrete Mean Value of the Derivative of the Riemann Zeta Function
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 113-155
- Print publication:
- December 2007
-
- Article
- Export citation
A New Unconditional Result about Large Spaces Between Zeta Zeros
- Part of
-
- Journal:
- Mathematika / Volume 52 / Issue 1-2 / December 2005
- Published online by Cambridge University Press:
- 21 December 2009, pp. 101-113
- Print publication:
- December 2005
-
- Article
- Export citation
Certain functional relations for the double harmonic series related to the double Euler numbers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 319-333
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
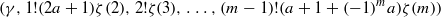

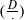 . As a consequence, using the identities of Cohen [‘Sums involving the values at negative integers of
. As a consequence, using the identities of Cohen [‘Sums involving the values at negative integers of 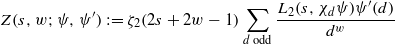
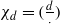 and the subscript 2 denotes the fact that the Euler factor at 2 has been removed. These double Dirichlet series can be extended to
and the subscript 2 denotes the fact that the Euler factor at 2 has been removed. These double Dirichlet series can be extended to 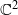 possessing a group of functional equations isomorphic to
possessing a group of functional equations isomorphic to