Refine listing
Actions for selected content:
230 results in 11Mxx
SINGLE-VALUED MOTIVIC PERIODS AND MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 October 2014, e25
-
- Article
-
- You have access
- Open access
- Export citation
ON WITTEN MULTIPLE ZETA-FUNCTIONS ASSOCIATED WITH SEMI-SIMPLE LIE ALGEBRAS V
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 26 August 2014, pp. 107-130
- Print publication:
- January 2015
-
- Article
-
- You have access
- Export citation
Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 257-273
-
- Article
-
- You have access
- Export citation
Nonvanishing of twists of
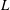 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$-functions attached to Hilbert modular forms
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$-functions attached to Hilbert modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 330-348
-
- Article
-
- You have access
- Export citation
A FAMILY OF MULTIPLE HARMONIC SUM AND MULTIPLE ZETA STAR VALUE IDENTITIES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 28 May 2014, pp. 63-71
- Print publication:
- January 2015
-
- Article
- Export citation
Subconvexity and equidistribution of Heegner points in the level aspect
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 17 June 2013, pp. 1150-1174
- Print publication:
- July 2013
-
- Article
- Export citation
NEGATIVE VALUES OF THE RIEMANN ZETA FUNCTION ON THE CRITICAL LINE
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 17 June 2013, pp. 443-462
- Print publication:
- July 2013
-
- Article
- Export citation
A NEW UPPER BOUND FOR
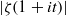 $\vert \zeta (1+ it)\vert $
$\vert \zeta (1+ it)\vert $
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 259-264
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
Pretentious multiplicative functions and the prime number theorem for arithmetic progressions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 14 May 2013, pp. 1129-1149
- Print publication:
- July 2013
-
- Article
- Export citation
Complex B-splines and Hurwitz zeta functions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 10 April 2013, pp. 61-77
-
- Article
-
- You have access
- Export citation
Logarithmic derivatives of Artin
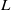 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 568-586
- Print publication:
- April 2013
-
- Article
- Export citation
Computing zeta functions of nondegenerate hypersurfaces with few monomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 9-44
-
- Article
-
- You have access
- Export citation
ZEROS OF THE ESTERMANN ZETA FUNCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 01 March 2013, pp. 38-49
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
CONTINUOUS LOWER BOUNDS FOR MOMENTS OF ZETA AND L-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 15 November 2012, pp. 119-128
- Print publication:
- January 2013
-
- Article
- Export citation
BETWEEN THE PROBLEMS OF PÓLYA AND TURÁN
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 27 September 2012, pp. 157-171
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Sato–Tate distributions and Galois endomorphism modules in genus 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1390-1442
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
JOINT UNIVERSALITY OF HURWITZ ZETA-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 09 July 2012, pp. 232-243
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Averages of shifted convolutions of d3(n)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 551-576
-
- Article
-
- You have access
- Export citation
The L2 restriction norm of a GL3 Maass form
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 20 March 2012, pp. 675-717
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
On the convergence of Diophantine Dirichlet series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 513-541
-
- Article
-
- You have access
- Export citation
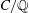

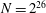
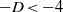
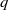
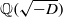
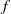
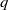
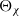
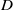
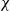
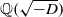
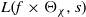
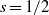
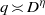
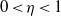
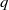
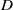
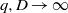
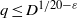
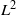
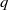
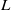
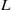
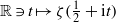
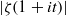
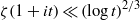
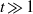
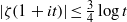
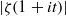
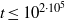




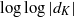
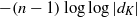
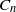
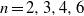
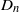
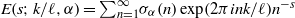


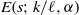
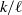

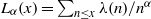
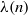

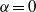
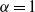
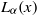
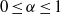
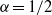
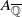 (the
(the 