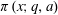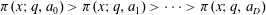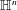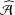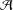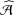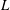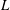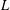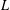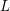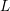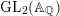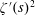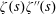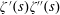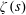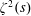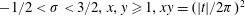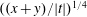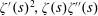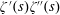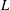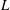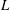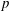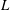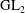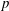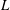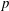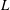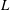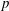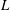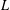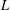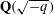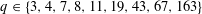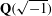Refine listing
Actions for selected content:
230 results in 11Mxx
Limiting Properties of the Distribution of Primes in an Arbitrarily Large Number of Residue Classes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 837-849
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Ideal Uniform Polyhedra in
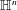 $\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
$\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 465-492
- Print publication:
- April 2021
-
- Article
- Export citation
DERIVATION RELATION FOR FINITE MULTIPLE ZETA VALUES IN
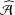 $\widehat{{\mathcal{A}}}$
$\widehat{{\mathcal{A}}}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 January 2020, pp. 260-265
- Print publication:
- April 2021
-
- Article
- Export citation
Moments of the Dedekind zeta function and other non-primitive L-functions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 November 2019, pp. 191-219
- Print publication:
- January 2021
-
- Article
- Export citation
Cotangent Sums Related to the Riemann Hypothesis for Various Shifts of the Argument
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 15 October 2019, pp. 522-535
- Print publication:
- September 2020
-
- Article
-
- You have access
- Open access
- Export citation
One-Level Density of Low-lying Zeros of Quadratic and Quartic Hecke
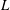 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 August 2019, pp. 427-454
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
SATO–TATE EQUIDISTRIBUTION OF CERTAIN FAMILIES OF ARTIN
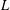 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 August 2019, e23
-
- Article
-
- You have access
- Open access
- Export citation
ON A GENERALISATION OF A RESTRICTED SUM FORMULA FOR MULTIPLE ZETA VALUES AND FINITE MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 July 2019, pp. 23-34
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
SYMMETRIC FUNCTIONS AND MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 24 July 2019, pp. 426-437
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Simple zeros of automorphic
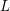 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 30 May 2019, pp. 1224-1243
- Print publication:
- June 2019
-
- Article
- Export citation
Many odd zeta values are irrational
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 26 April 2019, pp. 938-952
- Print publication:
- May 2019
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Lambert series and arithmetic nature of odd zeta values
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 24 January 2019, pp. 741-769
- Print publication:
- April 2020
-
- Article
- Export citation
Explicit asymptotics for certain single and double exponential sums
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 22 January 2019, pp. 607-632
- Print publication:
- April 2020
-
- Article
- Export citation
The fifth moment of Hecke L-functions in the weight aspect
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 168 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 14 January 2019, pp. 543-566
- Print publication:
- May 2020
-
- Article
- Export citation
Titchmarsh’s Method for the Approximate Functional Equations for
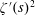 $\unicode[STIX]{x1D701}^{\prime }(s)^{2}$,
$\unicode[STIX]{x1D701}^{\prime }(s)^{2}$, 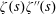 $\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and
$\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and 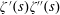 $\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$
$\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1465-1493
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Weighted Distribution of Low-lying Zeros of GL(2)
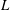 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 08 January 2019, pp. 153-182
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
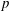 $p$-adic
$p$-adic 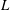 $L$-functions for
$L$-functions for 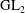 $\text{GL}_{2}$
$\text{GL}_{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1019-1059
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
One Level Density for Cubic Galois Number Fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 149-167
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
QUANTITATIVE ESTIMATES FOR SIMPLE ZEROS OF
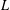 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 375-399
- Print publication:
- 2019
-
- Article
- Export citation
CLASS NUMBER ONE FROM ANALYTIC RANK TWO
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 03 January 2019, pp. 333-374
- Print publication:
- 2019
-
- Article
- Export citation