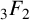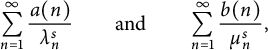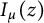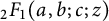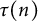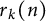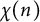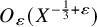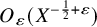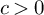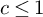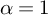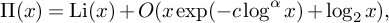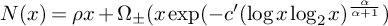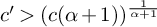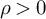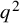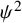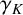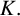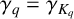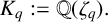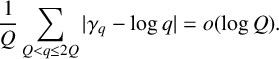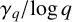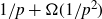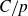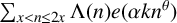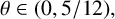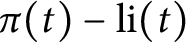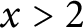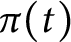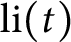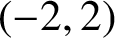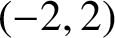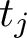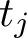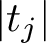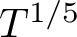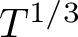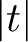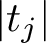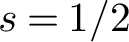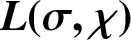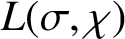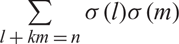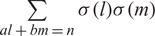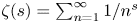Refine listing
Actions for selected content:
230 results in 11Mxx
OHNO–ZAGIER TYPE RELATIONS FOR MULTIPLE t-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 215-226
- Print publication:
- April 2023
-
- Article
- Export citation
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two general series identities involving modified Bessel functions and a class of arithmetical functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 10 October 2022, pp. 1800-1830
- Print publication:
- December 2023
-
- Article
- Export citation
Omega results for cubic field counts via lower-order terms in the one-level density
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 September 2022, e80
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE OPTIMAL MALLIAVIN-TYPE REMAINDER FOR BEURLING GENERALIZED INTEGERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 August 2022, pp. 249-278
- Print publication:
- January 2024
-
- Article
- Export citation
Motohashi’s formula for the fourth moment of individual Dirichlet L-functions and applications
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EULER–KRONECKER CONSTANTS FOR CYCLOTOMIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 79-84
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random symmetric matrices: rank distribution and irreducibility of the characteristic polynomial
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 May 2022, pp. 233-246
- Print publication:
- March 2023
-
- Article
- Export citation
AVERAGES OF EXPONENTIAL TWISTS OF THE VON MANGOLDT FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 425-430
- Print publication:
- December 2022
-
- Article
- Export citation
On the average value of
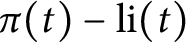 $\pi (t)-\operatorname {\textrm {li}}(t)$
$\pi (t)-\operatorname {\textrm {li}}(t)$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 March 2022, pp. 185-195
- Print publication:
- March 2023
-
- Article
- Export citation
LOWER-ORDER TERMS OF THE ONE-LEVEL DENSITY OF A FAMILY OF QUADRATIC HECKE
 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 22 February 2022, pp. 178-221
- Print publication:
- April 2023
-
- Article
- Export citation
EULER PRODUCT ASYMPTOTICS FOR DIRICHLET
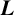 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 07 January 2022, pp. 48-56
- Print publication:
- August 2022
-
- Article
- Export citation
MOMENTS AND HYBRID SUBCONVEXITY FOR SYMMETRIC-SQUARE L-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 06 December 2021, pp. 2029-2073
- Print publication:
- September 2023
-
- Article
- Export citation
Nonvanishing for cubic L-functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 October 2021, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON LARGE VALUES OF
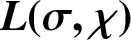 $\boldsymbol{L(\sigma ,\chi )}$
$\boldsymbol{L(\sigma ,\chi )}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 04 October 2021, pp. 412-418
- Print publication:
- June 2022
-
- Article
- Export citation
A generalized Davenport expansion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 26 August 2021, pp. 711-715
-
- Article
- Export citation
EVALUATION OF CONVOLUTION SUMS
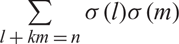 $$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND
$$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND 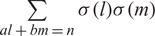 $$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
$$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 434-453
- Print publication:
- May 2022
-
- Article
- Export citation
Une note sur la densité des zéros des sommes partielles de la fonction zeta de Dedekind sur un corps quadratique
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 409-415
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prime geodesics and averages of the Zagier L-series
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 705-728
- Print publication:
- May 2022
-
- Article
- Export citation
Fourier transforms related to ζ(s)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 200-216
-
- Article
- Export citation