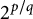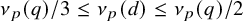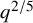Refine listing
Actions for selected content:
230 results in 11Mxx
Inequalities for the sequences with unified form
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 November 2025, pp. 1-20
-
- Article
- Export citation
On the Hilbert space derived from the Weil distribution
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inequality arising from the iterated Laguerre operator for various partitions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 23 October 2025, pp. 1-22
-
- Article
- Export citation
Explicit spectral gap for Hecke congruence covers of arithmetic Schottky surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 26 September 2025, pp. 1-41
-
- Article
- Export citation
A note on twisted moments of Dirichlet
 $\boldsymbol{L}$-functions
$\boldsymbol{L}$-functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 September 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On moments of L-functions over Dirichlet characters
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-24
-
- Article
- Export citation
Oscillation results for the summatory functions of fake
 $\mu $’s
$\mu $’s
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit theorems for a class of unbounded observables with an application to ‘Sampling the Lindelöf hypothesis’
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 12 August 2025, pp. 34-92
- Print publication:
- January 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting cyclic extensions with local conditions and applications to L-values in the critical strip
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-39
-
- Article
- Export citation
AN ASYMPTOTIC ESTIMATE FOR THE CHARACTERISTIC AND NUMBER OF FIXED POINTS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 01 August 2025, pp. 648-665
- Print publication:
- December 2025
-
- Article
- Export citation
Revisiting Dwork cohomology: visibility and divisibility of Frobenius eigenvalues in rigid cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1215-1249
- Print publication:
- June 2025
-
- Article
-
- You have access
- HTML
- Export citation
A criterion for the simple normality of fractional powers of two via the Riemann zeta function
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 29 May 2025, pp. 1-24
-
- Article
- Export citation
Euler Products at the Centre and Applications to Chebyshev’s Bias
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 27 May 2025, pp. 331-349
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic second moment of Dirichlet L-functions along a thin coset
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 02 May 2025, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symmetric multiple zeta functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shifted moments of quadratic Dirichlet L-functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1116-1143
- Print publication:
- December 2025
-
- Article
- Export citation
ON SOME EFFECTIVE RESULTS INVOLVING ZEROS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 563-565
- Print publication:
- June 2025
-
- Article
-
- You have access
- HTML
- Export citation
TWISTED RUELLE ZETA FUNCTION ON HYPERBOLIC MANIFOLDS AND COMPLEX-VALUED ANALYTIC TORSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 813-845
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DERIVATIVES OF THETA FUNCTIONS AS TRACES OF PARTITION EISENSTEIN SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 284-295
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME CASES OF OORT’S CONJECTURE ABOUT NEWTON POLYGONS OF CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 93-103
- Print publication:
- March 2025
-
- Article
- Export citation