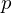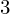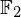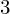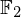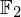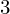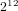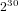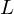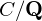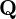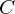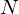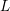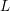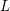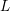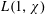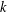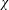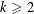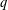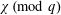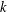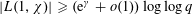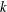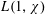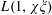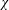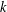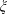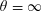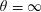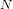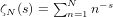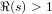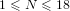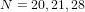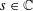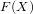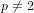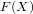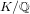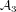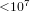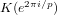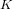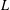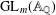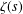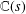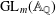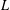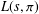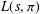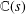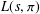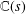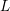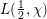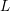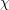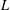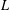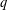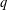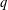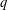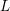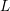Refine listing
Actions for selected content:
230 results in 11Mxx
Point counting on K3 surfaces and an application concerning real and complex multiplication
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 12-28
-
- Article
-
- You have access
- Export citation
A census of zeta functions of quartic K
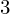 $3$ surfaces over
$3$ surfaces over 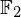 $\mathbb{F}_{2}$
$\mathbb{F}_{2}$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 1-11
-
- Article
-
- You have access
- Export citation
Character theory approach to Sato–Tate groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 301-314
-
- Article
-
- You have access
- Export citation
Computing
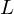 $L$ -series of geometrically hyperelliptic curvesof genus three
$L$ -series of geometrically hyperelliptic curvesof genus three
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 220-234
-
- Article
-
- You have access
- Export citation
PAIR CORRELATION OF LOW-LYING ZEROS OF QUADRATIC
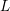 $L$ -FUNCTIONS
$L$ -FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 223 / Issue 1 / September 2016
- Published online by Cambridge University Press:
- 18 August 2016, pp. 87-135
- Print publication:
- September 2016
-
- Article
-
- You have access
- HTML
- Export citation
LARGE VALUES OF
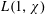 $L(1,\unicode[STIX]{x1D712})$ FOR
$L(1,\unicode[STIX]{x1D712})$ FOR 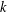 $k$ TH ORDER CHARACTERS
$k$ TH ORDER CHARACTERS 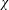 $\unicode[STIX]{x1D712}$ AND APPLICATIONS TO CHARACTER SUMS
$\unicode[STIX]{x1D712}$ AND APPLICATIONS TO CHARACTER SUMS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 July 2016, pp. 53-71
- Print publication:
- 2017
-
- Article
- Export citation
THE
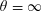 $\unicode[STIX]{x1D703}=\infty$ CONJECTURE IMPLIES THE RIEMANN HYPOTHESIS
$\unicode[STIX]{x1D703}=\infty$ CONJECTURE IMPLIES THE RIEMANN HYPOTHESIS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 July 2016, pp. 29-33
- Print publication:
- 2017
-
- Article
- Export citation
Zeroes of partial sums of the zeta-function
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 37-41
-
- Article
-
- You have access
- Export citation
OPPOSITE-SIGN KLOOSTERMAN SUM ZETA FUNCTION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 28 January 2016, pp. 406-429
- Print publication:
- 2016
-
- Article
- Export citation
SIGN OF FOURIER COEFFICIENTS OF MODULAR FORMS OF HALF-INTEGRAL WEIGHT
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 866-883
- Print publication:
- 2016
-
- Article
- Export citation
On
 ${\it\lambda}$ -invariants attached to cyclic cubic number fields
${\it\lambda}$ -invariants attached to cyclic cubic number fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 684-698
-
- Article
-
- You have access
- Export citation
HYPERTRANSCENDENCE OF
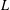 $L$-FUNCTIONS FOR
$L$-FUNCTIONS FOR 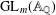 $\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$
$\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 388-399
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
ON MULTIPLE ZETA VALUES OF EXTREMAL HEIGHT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 186-193
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Sub-Weyl subconvexity for Dirichlet
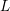 $L$-functions to prime power moduli
$L$-functions to prime power moduli
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 825-875
- Print publication:
- April 2016
-
- Article
- Export citation
A NOTE ON SIMPLE ZEROS OF PRIMITIVE DIRICHLET
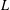 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 19-30
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
UNFOLDING THE DOUBLE SHUFFLE STRUCTURE OF
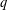 $q$-MULTIPLE ZETA VALUES
$q$-MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 24 April 2015, pp. 368-388
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
On certain mean values of the double zeta-function
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 217 / March 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 161-190
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
INFINITE PRODUCTS OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 400-411
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
UNIQUENESS THEOREMS FOR DIRICHLET SERIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 12 February 2015, pp. 389-399
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Unnormalized differences between zeros of L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 230-252
- Print publication:
- February 2015
-
- Article
- Export citation