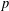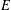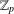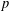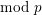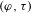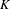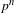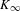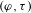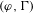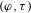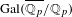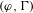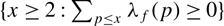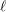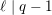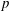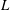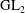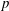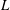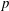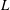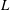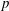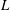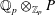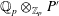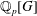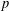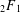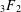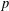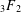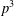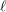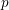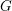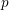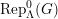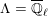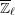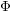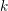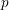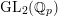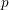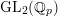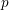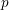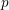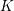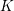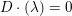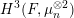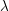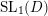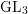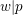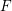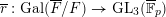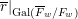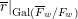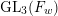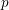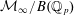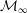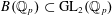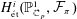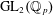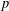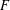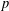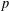Refine listing
Actions for selected content:
122 results in 11Sxx
DEFORMATION CONDITIONS FOR PSEUDOREPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 18 July 2019, e20
-
- Article
-
- You have access
- Open access
- Export citation
ON THE EULER CHARACTERISTICS OF SIGNED SELMER GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 09 July 2019, pp. 238-246
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
REFINED SWAN CONDUCTORS
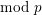 $\text{mod}~p$ OF ONE-DIMENSIONAL GALOIS REPRESENTATIONS
$\text{mod}~p$ OF ONE-DIMENSIONAL GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 03 June 2019, pp. 134-182
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
LOCALLY ANALYTIC VECTORS AND OVERCONVERGENT
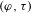 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-MODULES
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 03 May 2019, pp. 137-185
- Print publication:
- January 2021
-
- Article
- Export citation
COHOMOLOGY AND OVERCONVERGENCE FOR REPRESENTATIONS OF POWERS OF GALOIS GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 11 April 2019, pp. 361-421
- Print publication:
- March 2021
-
- Article
- Export citation
Chebyshev’s bias for analytic L-functions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 22 March 2019, pp. 103-140
- Print publication:
- July 2020
-
- Article
- Export citation
Cohen–Lenstra heuristics for étale group schemes and symplectic pairings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 4 / April 2019
- Published online by Cambridge University Press:
- 20 March 2019, pp. 758-775
- Print publication:
- April 2019
-
- Article
- Export citation
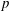 $p$-adic
$p$-adic 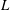 $L$-functions for
$L$-functions for 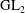 $\text{GL}_{2}$
$\text{GL}_{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1019-1059
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
A Generalization of a Theorem of Swan with Applications to Iwasawa Theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 16 November 2018, pp. 656-675
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
SUPERCONGRUENCES INVOLVING
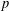 $p$ -ADIC GAMMA FUNCTIONS
$p$ -ADIC GAMMA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 30 May 2018, pp. 27-37
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Sur les
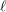 $\ell$ -blocs de niveau zéro des groupes
$\ell$ -blocs de niveau zéro des groupes 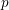 $p$ -adiques
$p$ -adiques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 24 May 2018, pp. 1473-1507
- Print publication:
- July 2018
-
- Article
- Export citation
GROUP ACTION ON THE DEFORMATIONS OF A FORMAL GROUP OVER THE RING OF WITT VECTORS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 20 December 2017, pp. 42-57
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
Patching and the
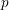 $p$ -adic Langlands program for
$p$ -adic Langlands program for 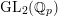 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 01 December 2017, pp. 503-548
- Print publication:
- March 2018
-
- Article
- Export citation
Local–global principle for reduced norms over function fields of
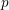 $p$ -adic curves
$p$ -adic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 410-458
- Print publication:
- February 2018
-
- Article
- Export citation
On mod
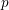 $p$ local-global compatibility for
$p$ local-global compatibility for 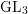 $\text{GL}_{3}$ in the ordinary case
$\text{GL}_{3}$ in the ordinary case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 25 August 2017, pp. 2215-2286
- Print publication:
- November 2017
-
- Article
- Export citation
RAMIFICATION IN KUMMER EXTENSIONS ARISING FROM ALGEBRAIC TORI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 196-204
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
A QUOTIENT OF THE LUBIN–TATE TOWER
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 27 July 2017, e17
-
- Article
-
- You have access
- Open access
- Export citation
Stable vectors in Moy–Prasad filtrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 09 February 2017, pp. 358-372
- Print publication:
- February 2017
-
- Article
- Export citation
SERRE WEIGHTS AND WILD RAMIFICATION IN TWO-DIMENSIONAL GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 23 December 2016, e33
-
- Article
-
- You have access
- Open access
- Export citation
ON GALOIS EQUIVARIANCE OF HOMOMORPHISMS BETWEEN TORSION CRYSTALLINE REPRESENTATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 13 December 2016, pp. 169-214
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation