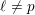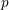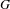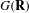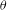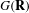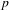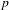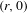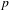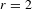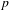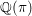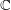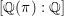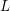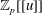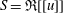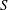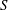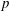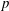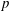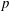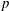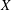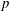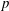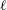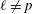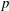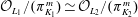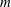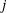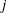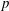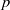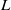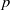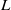Refine listing
Actions for selected content:
122 results in 11Sxx
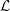 ${\mathcal{L}}$ -INVARIANTS AND LOCAL–GLOBAL COMPATIBILITY FOR THE GROUP
${\mathcal{L}}$ -INVARIANTS AND LOCAL–GLOBAL COMPATIBILITY FOR THE GROUP 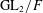 $\text{GL}_{2}/F$
$\text{GL}_{2}/F$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 10 June 2016, e13
-
- Article
-
- You have access
- Open access
- Export citation
An application of the
 $p$ -adic analytic class number formula
$p$ -adic analytic class number formula
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 217-228
-
- Article
-
- You have access
- Export citation
Density of potentially crystalline representations of fixed weight
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 1609-1647
- Print publication:
- August 2016
-
- Article
- Export citation
WILDER MCKAY CORRESPONDENCES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 221 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 15 March 2016, pp. 111-164
- Print publication:
- March 2016
-
- Article
-
- You have access
- HTML
- Export citation
COUNTING POINTS ON DWORK HYPERSURFACES AND
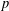 $p$ -ADIC HYPERGEOMETRIC FUNCTIONS
$p$ -ADIC HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 208-216
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Sub-Weyl subconvexity for Dirichlet
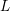 $L$-functions to prime power moduli
$L$-functions to prime power moduli
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 825-875
- Print publication:
- April 2016
-
- Article
- Export citation
A DEFINABLE
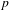 $p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
$p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 October 2015, pp. 39-57
- Print publication:
- February 2018
-
- Article
- Export citation
Optimal cycles in ultrametric dynamics and minimally ramified power series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 187-222
- Print publication:
- January 2016
-
- Article
- Export citation
TOPOLOGY ON COHOMOLOGY OF LOCAL FIELDS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 25 August 2015, e16
-
- Article
-
- You have access
- Open access
- Export citation
On p-adic analytic continuation with applications to generating elements
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 10 June 2015, pp. 1-10
-
- Article
- Export citation
Compatibility of arithmetic and algebraic local constants (the case
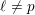 $\ell \neq p$)
$\ell \neq p$)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 9 / September 2015
- Published online by Cambridge University Press:
- 08 April 2015, pp. 1626-1646
- Print publication:
- September 2015
-
- Article
- Export citation
Coleman integration for even-degree models of hyperelliptic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 258-265
-
- Article
-
- You have access
- Export citation
TEMPERED SPECTRAL TRANSFER IN THE TWISTED ENDOSCOPY OF REAL GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 17 December 2014, pp. 569-612
- Print publication:
- July 2016
-
- Article
- Export citation
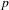 $p$-ADIC EISENSTEIN SERIES AND
$p$-ADIC EISENSTEIN SERIES AND  $L$-FUNCTIONS OF CERTAIN CUSP FORMS ON DEFINITE UNITARY GROUPS
$L$-FUNCTIONS OF CERTAIN CUSP FORMS ON DEFINITE UNITARY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 21 November 2014, pp. 471-510
- Print publication:
- July 2016
-
- Article
- Export citation
On fields of rationality for automorphic representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 11 September 2014, pp. 2003-2053
- Print publication:
- December 2014
-
- Article
- Export citation
Linear algebra over
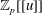 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 302-344
-
- Article
-
- You have access
- Export citation
The
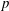 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 10 June 2014, pp. 1125-1168
- Print publication:
- July 2014
-
- Article
- Export citation
Product formula for p -adic epsilon factors
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 08 May 2014, pp. 275-377
- Print publication:
- April 2015
-
- Article
- Export citation
Ramification theory and perfectoid spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 03 April 2014, pp. 798-834
- Print publication:
- May 2014
-
- Article
- Export citation
Trivial zeros of
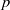 $p$ -adic
$p$ -adic 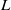 $L$ -functions at near-central points
$L$ -functions at near-central points
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 24 September 2013, pp. 561-598
- Print publication:
- July 2014
-
- Article
- Export citation
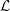
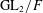
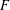
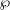
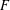
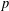
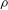
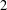
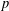
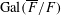
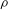
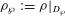
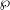
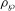
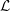
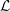
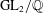


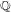

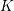
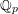
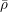
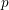
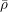
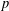
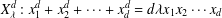
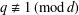
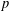
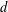
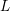
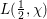
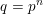
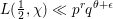

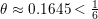
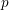
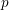
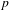
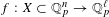
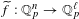
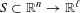
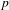
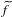
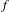
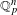
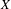
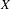
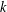
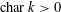
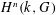
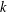
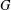
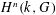
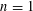
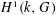
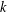
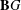
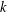
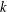
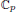 , the topological completion of the algebraic closure of the field of
, the topological completion of the algebraic closure of the field of