Refine listing
Actions for selected content:
122 results in 11Sxx
Self-dual integral normal bases and Galois module structure
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 10 May 2013, pp. 1175-1202
- Print publication:
- July 2013
-
- Article
- Export citation
On the Iwasawa theory of the Lubin–Tate moduli space
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 793-839
- Print publication:
- May 2013
-
- Article
- Export citation
On the gcd of local Rankin–Selberg integrals for even orthogonal groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 20 December 2012, pp. 587-636
- Print publication:
- April 2013
-
- Article
- Export citation
Minimal models for rational functions in a dynamical setting
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 December 2012, pp. 400-417
-
- Article
-
- You have access
- Export citation
Structures de Hodge–Pink pour les φ/𝔖-modules de Breuil et Kisin
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 03 May 2012, pp. 751-789
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
On modular inverses of cyclotomic polynomials and the magnitude oftheir coefficients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 April 2012, pp. 44-58
-
- Article
-
- You have access
- Export citation
A SIMPLIFIED PROOF OF HESSELHOLT’S CONJECTURE ON GALOIS COHOMOLOGY OF WITT VECTORS OF ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 25 January 2012, pp. 456-460
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
On ramification filtrations and p-adic differential equations, II: mixed characteristic case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 415-463
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Remarks on endomorphisms and rational points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 24 August 2011, pp. 1819-1842
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation
Extensions of rank one (φ,Γ)-modules and crystalline representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 13 December 2010, pp. 375-427
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
A p-adic analogue of the Borel regulator and the Bloch–Kato exponential map
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 05 August 2010, pp. 149-190
- Print publication:
- January 2011
-
- Article
- Export citation
Local Fourier transform and epsilon factors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 6 / November 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 1507-1551
- Print publication:
- November 2010
-
- Article
-
- You have access
- Export citation
Affine Deligne–Lusztig varieties in affine flag varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 07 July 2010, pp. 1339-1382
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Swan conductors for p-adic differential modules. II Global variation
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 11 May 2010, pp. 191-224
- Print publication:
- January 2011
-
- Article
- Export citation
Classification of two-dimensional split trianguline representations of p-adic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 865-914
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
Formule du conducteur pour un caractère l-adique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 687-717
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
p-units in ray class fields of real quadratic number fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 364-392
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Presque Cp-représentations et (ϕ,Γ)-modules
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 653-668
- Print publication:
- October 2009
-
- Article
- Export citation
Wild ramification and the characteristic cycle of an ℓ-adic sheaf
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 06 January 2009, pp. 769-829
- Print publication:
- October 2009
-
- Article
- Export citation
Analytic vectors in continuous p-adic representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 247-270
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
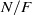
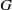
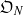
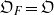
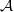
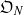
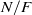
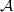
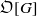
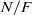
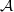
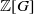
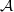
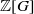
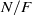
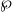
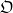
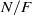
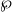
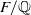
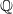
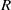
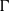
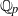
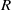
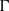
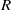
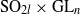
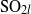
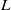
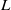
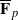 -representations of
-representations of 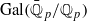 for
for 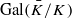 using
using 