Refine listing
Actions for selected content:
112 results in 11Txx
A POLYNOMIAL APPROACH TO COCYCLES OVER ELEMENTARY ABELIAN GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 177-190
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Extending abelian groups to rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-314
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Am-permutation polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-158
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
On decomposition of sub-linearised-polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 317-328
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
Multiplicities of Higher Lie Characters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 9-21
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Engel Series Expansions of Laurent Series and Hausdorff Dimensions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-7
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Counting irreducible Goppa codes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 299-306
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Asymptotics of poisson approximation to random discrete distributions: an analytic approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 448-491
- Print publication:
- June 1999
-
- Article
- Export citation
Estimates of hybrid exponential sums on quasiprojective varieties over finite fields
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-72
- Print publication:
- June 1996
-
- Article
- Export citation
The value set of polynomials over ℤm and the combinatorics of sequences
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 190-198
- Print publication:
- June 1995
-
- Article
- Export citation
On Schur's conjecture
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 3 / June 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 312-357
- Print publication:
- June 1995
-
- Article
-
- You have access
- Export citation
The factorable core of polynomials over finite fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 309-318
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
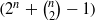 -dimensional GF(2
-dimensional GF(2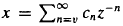 in an inderminate
in an inderminate 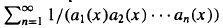 be the Engel expansin of Laurent series of
be the Engel expansin of Laurent series of 