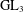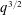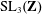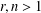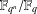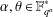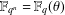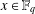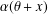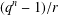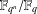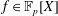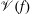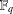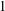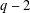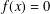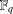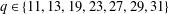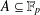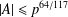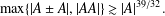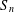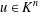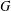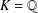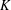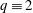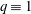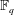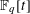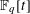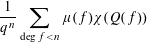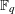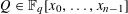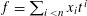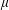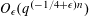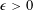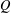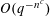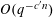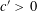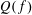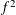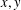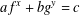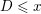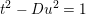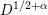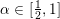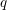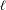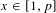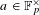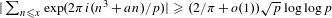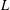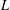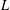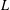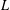Refine listing
Actions for selected content:
112 results in 11Txx
PERIODIC TWISTS OF
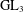 $\operatorname{GL}_{3}$-AUTOMORPHIC FORMS
$\operatorname{GL}_{3}$-AUTOMORPHIC FORMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 12 March 2020, e15
-
- Article
-
- You have access
- Open access
- Export citation
FINITE FIELD EXTENSIONS WITH THE LINE OR TRANSLATE PROPERTY FOR
 $r$-PRIMITIVE ELEMENTS
$r$-PRIMITIVE ELEMENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 02 March 2020, pp. 313-319
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
LOWER BOUNDS FOR PERIODS OF DUCCI SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 22 November 2019, pp. 31-38
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Value Sets of Sparse Polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 24 September 2019, pp. 187-196
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
A NEW PROOF OF THE CARLITZ–LUTZ THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 10 July 2019, pp. 56-60
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
PERMUTATION POLYNOMIALS OF DEGREE 8 OVER FINITE FIELDS OF ODD CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 July 2019, pp. 40-55
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
A NEW SUM–PRODUCT ESTIMATE IN PRIME FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 24 May 2019, pp. 268-280
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
ON THE DIMENSION OF PERMUTATION VECTOR SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 03 April 2019, pp. 256-267
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Cubic Twin Prime Polynomials are Counted by a Modular Form
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1323-1350
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Irreducible Polynomials Over a Finite Field with Restricted Coefficients
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 429-439
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
HADAMARD MATRICES AND 1-FACTORIZATIONS OF COMPLETE GRAPHS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 11 February 2019, pp. 488-499
- Print publication:
- 2019
-
- Article
- Export citation
CANCELLATIONS BETWEEN KLOOSTERMAN SUMS MODULO A PRIME POWER WITH PRIME ARGUMENTS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 475-487
- Print publication:
- 2019
-
- Article
- Export citation
LINEAR AND QUADRATIC UNIFORMITY OF THE MÖBIUS FUNCTION OVER
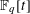 $\mathbb{F}_{q}[t]$
$\mathbb{F}_{q}[t]$
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 05 March 2019, pp. 505-529
- Print publication:
- 2019
-
- Article
- Export citation
ON FINDING SOLUTIONS TO EXPONENTIAL CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 388-391
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Counting fundamental solutions to the Pell equation with prescribed size
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 11 October 2018, pp. 2379-2402
- Print publication:
- November 2018
-
- Article
- Export citation
ON THE DISTRIBUTION OF THE MAXIMUM OF CUBIC EXPONENTIAL SUMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 27 September 2018, pp. 1259-1286
- Print publication:
- July 2020
-
- Article
- Export citation
THE RECIPROCITY LAW FOR THE TWISTED SECOND MOMENT OF DIRICHLET
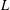 $L$ -FUNCTIONS OVER RATIONAL FUNCTION FIELDS
$L$ -FUNCTIONS OVER RATIONAL FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 28 August 2018, pp. 383-388
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Bounding the Number of Common Zeros of Multivariate Polynomials and Their Consecutive Derivatives
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 03 August 2018, pp. 253-279
-
- Article
- Export citation
A VARIATION ON THE THEME OF NICOMACHUS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 367-373
- Print publication:
- June 2018
-
- Article
-
- You have access
- Open access
- Export citation
On Zeros of a Polynomial in a Finite Grid
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 310-333
-
- Article
- Export citation