Refine listing
Actions for selected content:
112 results in 11Txx
ON CONFIGURATIONS WHERE THE LOOMIS–WHITNEY INEQUALITY IS NEARLY SHARP AND APPLICATIONS TO THE FURSTENBERG SET PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 07 January 2015, pp. 145-161
- Print publication:
- January 2015
-
- Article
- Export citation
Constructing abelian surfaces for cryptography via Rosenhain invariants
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 157-180
-
- Article
-
- You have access
- Export citation
The discrete logarithm problem for exponents of bounded height
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 148-156
-
- Article
-
- You have access
- Export citation
Finding roots in
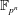 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_{p^n}$ with the successive resultants algorithm
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_{p^n}$ with the successive resultants algorithm
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 203-217
-
- Article
-
- You have access
- Export citation
The multiple number field sieve for medium- and high-characteristic finite fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 230-246
-
- Article
-
- You have access
- Export citation
ON THE EXPONENT OF DISTRIBUTION OF THE TERNARY DIVISOR FUNCTION
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 02 June 2014, pp. 121-144
- Print publication:
- January 2015
-
- Article
- Export citation
A NOTE ON INTERPOLATION OF PERMUTATIONS OF A SUBSET OF A FINITE FIELD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 213-219
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
CONSTRUCTING PERMUTATION POLYNOMIALS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 420-430
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
REPRESENTING AN ELEMENT IN
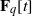 ${\mathbf{F} }_{q} [t] $ AS THE SUM OF TWO IRREDUCIBLES
${\mathbf{F} }_{q} [t] $ AS THE SUM OF TWO IRREDUCIBLES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 23 May 2013, pp. 166-182
- Print publication:
- January 2014
-
- Article
- Export citation
Extension and averaging operators for finite fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 April 2013, pp. 599-614
-
- Article
-
- You have access
- Export citation
ON PERMUTATION BINOMIALS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 28 March 2013, pp. 112-124
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
ELEMENTS OF LARGE ORDER IN PRIME FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 16 October 2012, pp. 169-176
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
Complete addition laws on abelian varieties
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 308-316
-
- Article
-
- You have access
- Export citation
SUM–PRODUCT ESTIMATES AND MULTIPLICATIVE ORDERS OF γ AND γ+γ−1 IN FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 505-508
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
ON THE CONSECUTIVE POWERS OF A PRIMITIVE ROOT: GAPS AND EXPONENTIAL SUMS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 08 November 2011, pp. 11-20
- Print publication:
- January 2012
-
- Article
- Export citation
EXPONENTIAL SUMS OVER POINTS OF ELLIPTIC CURVES WITH RECIPROCALS OF PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 13 July 2011, pp. 21-33
- Print publication:
- January 2012
-
- Article
- Export citation
ELEMENTS OF HIGH ORDER ON FINITE FIELDS FROM ELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 02 March 2010, pp. 425-429
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Explicit Kummer surface formulas for arbitrary characteristic
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 January 2010, pp. 47-64
-
- Article
-
- You have access
- Export citation
QUALIFIED DIFFERENCE SETS FROM UNIONS OF CYCLOTOMIC CLASSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 147-158
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
ARITHMETIC AND GEOMETRIC PROGRESSIONS IN PRODUCT SETS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 357-364
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
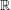
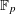
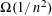
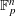
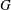

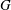
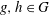

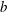
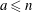
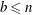
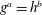
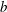
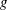
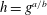
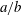

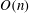
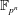
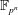
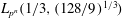
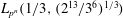
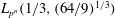
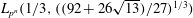
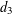
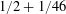
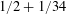
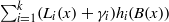
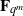
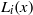
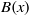
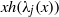
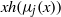
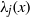
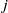
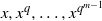
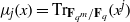
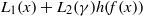
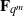
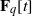
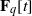

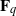
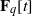

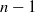
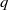


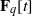
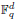 :
: 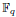 with
with 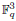 , due to Mockenhaupt and Tao, to the
, due to Mockenhaupt and Tao, to the 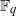
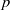
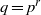
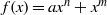
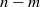
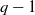
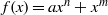
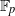
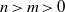
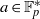
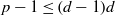
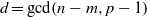
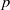
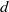
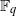
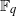
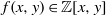
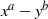
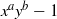
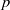
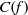
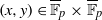
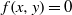
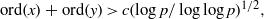

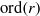

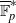
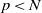
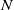
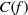
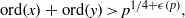
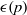
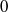
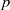
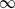
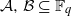 of elements of the finite field 𝔽
of elements of the finite field 𝔽