Refine listing
Actions for selected content:
2837 results in 11xxx
β-transformation, invariant measure and uniform distribution
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 418-428
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
On similar short sums
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 193-204
- Print publication:
- June 1999
-
- Article
- Export citation
Estimates of the least prime factor of a binomial coefficient
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 41-55
- Print publication:
- June 1999
-
- Article
- Export citation
Asymptotics of poisson approximation to random discrete distributions: an analytic approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 448-491
- Print publication:
- June 1999
-
- Article
- Export citation
Non-vanishing of the partition function modulo odd primes l
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-192
- Print publication:
- June 1999
-
- Article
- Export citation
The exact order of generalized diaphony and multidimensional numerical integration
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-17
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
The least primitive root mod 2p2
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 371-379
- Print publication:
- December 1998
-
- Article
- Export citation
Piatetski-Shapiro prime k-tuplets
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 351-357
- Print publication:
- December 1998
-
- Article
- Export citation
Sums of k-th powers in number fields
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 359-370
- Print publication:
- December 1998
-
- Article
- Export citation
Simultaneous diagonal p–adic equations
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 337-349
- Print publication:
- December 1998
-
- Article
- Export citation
On simultaneous additive equations, IV
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 319-335
- Print publication:
- December 1998
-
- Article
- Export citation
Non-expansive derived horseshoes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-415
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
Hardy's legacy to number theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 238-266
- Print publication:
- October 1998
-
- Article
-
- You have access
- Export citation
Involutions and commutators in orthogonal groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-36
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation
P-régularité de sommes d'exponentielles
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 145-175
- Print publication:
- June 1998
-
- Article
- Export citation
Application of the Bruhat-Tits tree of SU3(h) to some Ã2 groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 329-344
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Uniform bounds for the least almost-prime primitive root
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 191-207
- Print publication:
- June 1998
-
- Article
- Export citation
Uniformity over primes of unramified splittings
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 177-189
- Print publication:
- June 1998
-
- Article
- Export citation
On strings of consecutive integers with no large prime factors
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 266-276
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
Multiplicative isogeny estimates
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 178-194
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
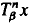 } are uniformly distributed. Here we consider the non-integer case, determine when
} are uniformly distributed. Here we consider the non-integer case, determine when 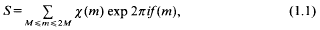
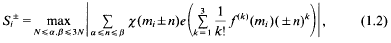

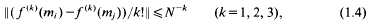
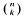 are >
are >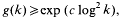
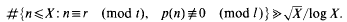
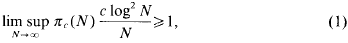
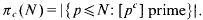
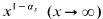 with
with 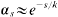 for large
for large 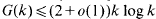 for large
for large 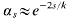 .
.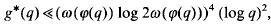
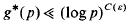
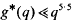 . However, there is not at present any stronger unconditional upper bound for
. However, there is not at present any stronger unconditional upper bound for 