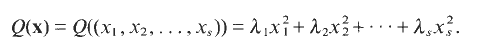Refine listing
Actions for selected content:
2838 results in 11xxx
On integers which are not differences of two powers
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-243
- Print publication:
- June 2002
-
- Article
- Export citation
On the representation of an integer as the sum of a large and a small square
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 245-251
- Print publication:
- June 2002
-
- Article
- Export citation
An analogue of Van der Corput's A5-process for exponential sums
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 167-183
- Print publication:
- June 2002
-
- Article
- Export citation
Small positive values of indefinite ternary forms
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-196
- Print publication:
- June 2002
-
- Article
- Export citation
The Hooley–Huxley contour method, for problems in number fields II: factorization and divisibility
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 201-225
- Print publication:
- June 2002
-
- Article
- Export citation
On shifted products which are powers
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 227-230
- Print publication:
- June 2002
-
- Article
- Export citation
Quick asymptotic upper bounds for lattice kissing numbers
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-57
- Print publication:
- June 2002
-
- Article
- Export citation
Lattice points on circles
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 217-222
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
The arithmetic of partitions into distinct parts
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 203-211
- Print publication:
- December 2001
-
- Article
- Export citation
The inverse Goldbach problem
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-158
- Print publication:
- December 2001
-
- Article
- Export citation
Gaussian primes in narrow sectors
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-135
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Irrational dilations of Pascal's triangle
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 159-168
- Print publication:
- December 2001
-
- Article
- Export citation
On simultaneous diagonal inequalities, II
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 191-202
- Print publication:
- December 2001
-
- Article
- Export citation
Counting irreducible Goppa codes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 299-306
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Character sums and the series L(1, χ)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-436
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
Fractional parts of Linear polynomials and an application to hypergeometric functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-424
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
Bases for cyclotomic units over function fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 56-70
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
Sums of three cubes
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 53-61
- Print publication:
- December 2000
-
- Article
- Export citation
Asymptotic lower bounds for Diophantine inequalities
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-159
- Print publication:
- December 2000
-
- Article
- Export citation
Sums of squares of integral linear forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 298-302
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation

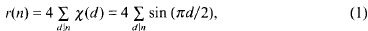

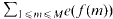 . The saving has now to be taken to the exponent 1/20 instead of 1/32. Our main application is a “ninth derivative test” for exponential sums which is essential for giving new exponent pairs in [3].
. The saving has now to be taken to the exponent 1/20 instead of 1/32. Our main application is a “ninth derivative test” for exponential sums which is essential for giving new exponent pairs in [3].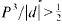 .
.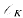 , the ring of integers of
, the ring of integers of 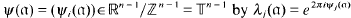 . Then the small region of
. Then the small region of 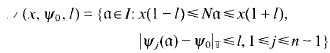
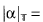 β. where β is the unique real satisyfing
β. where β is the unique real satisyfing 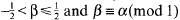 .
.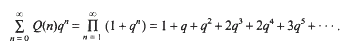
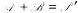 where, ℝ′ differs from the set of primes in finitely many elements only and
where, ℝ′ differs from the set of primes in finitely many elements only and 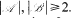 .
.