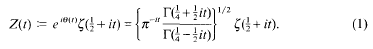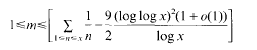Refine listing
Actions for selected content:
2838 results in 11xxx
Combinatorics and linear algebra of Freiman's isomorphism
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-51
- Print publication:
- December 2000
-
- Article
- Export citation
Frequency of oscillations of an error term related to the Euler function
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-164
- Print publication:
- December 2000
-
- Article
- Export citation
Un nouveau critère pour l'équation de Catalan
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-73
- Print publication:
- December 2000
-
- Article
- Export citation
Double circulant constructions of the Leech lattice
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-297
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
Character sums with exponential functions
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 75-85
- Print publication:
- December 2000
-
- Article
- Export citation
The order of inverses mod q
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-108
- Print publication:
- December 2000
-
- Article
- Export citation
Bh [g] sequences
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 109-115
- Print publication:
- December 2000
-
- Article
- Export citation
Additive representation in thin sequences, II: The binary Goldbach problem
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-125
- Print publication:
- December 2000
-
- Article
- Export citation
Classes of integral 3-tensors on 2-space
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 205-217
- Print publication:
- December 2000
-
- Article
- Export citation
Independance algebrique des derivees d'une periode du module de Carlitz
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 8-18
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
Theta series liftings from orthogonal groups to semi-simple groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 127-142
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
Apéry sequences and legendre transforms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-356
- Print publication:
- June 2000
-
- Article
-
- You have access
- Export citation
On integers with identical digits
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 411-417
- Print publication:
- December 1999
-
- Article
- Export citation
On extending Artin's conjecture to composite moduli
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 373-390
- Print publication:
- December 1999
-
- Article
- Export citation
On the scarcity of powerful binomial coefficients
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 397-410
- Print publication:
- December 1999
-
- Article
- Export citation
Sign changes of error terms related to the Euler function
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 391-395
- Print publication:
- December 1999
-
- Article
- Export citation
The behaviour of the Riemann zeta-function on the critical line
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 281-313
- Print publication:
- December 1999
-
- Article
- Export citation
On some questions of Erdős and Graham about Egyptian fractions
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 359-372
- Print publication:
- December 1999
-
- Article
- Export citation
On the divisor function d(n): II
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 419-423
- Print publication:
- December 1999
-
- Article
- Export citation
Notes on Erdös-Turán inequality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-57
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
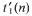 of classes of such cardinality
of classes of such cardinality 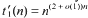 .
.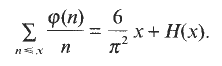

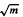 in the Leech lattice. We give such a construction by means of double circulant codes whenever
in the Leech lattice. We give such a construction by means of double circulant codes whenever 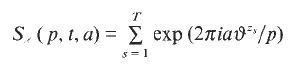
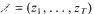 a sequence such that
a sequence such that 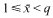 be such that
be such that 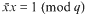 . For fixed
. For fixed 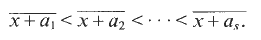
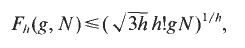
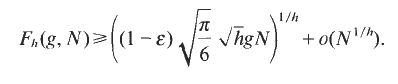
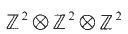 under the standard action of
under the standard action of 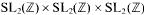 . A notion of primitivity is defined in this space and the number of primitive classes of a given discriminant is evaluated in terms of the class number of primitive binary quadratic forms of the same discriminant. Classes containing symmetric 3-tensors are also considered and their number is related to the 3-rank of the class group.
. A notion of primitivity is defined in this space and the number of primitive classes of a given discriminant is evaluated in terms of the class number of primitive binary quadratic forms of the same discriminant. Classes containing symmetric 3-tensors are also considered and their number is related to the 3-rank of the class group.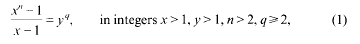
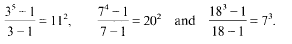
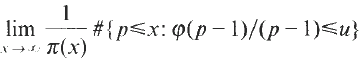
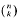 with 3≤
with 3≤ . Unconditionally, it is shown that there are
. Unconditionally, it is shown that there are 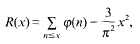
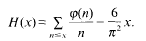
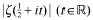 between successive zeros. Our results are to be independent of any unproved hypothesis. Put
between successive zeros. Our results are to be independent of any unproved hypothesis. Put